Conducting loop
A battery is connected to the endpoints A and B of a homogeneous wire. Using an ammeter one finds that a current
I
=
1
.
5
A
flows through the conductor.
Then, the wire is bent in the form of a circle and the same battery is connected to points A and B.
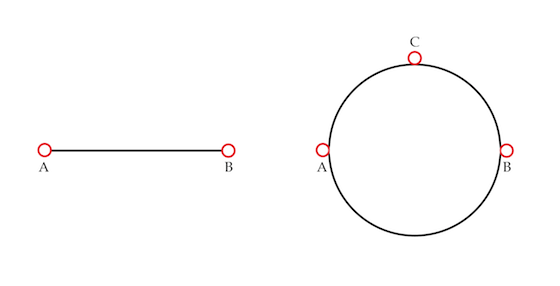 What is the current
in Amps
flowing through point C in this case? You may neglect the internal resistance of the battery.
What is the current
in Amps
flowing through point C in this case? You may neglect the internal resistance of the battery.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
the circle is connected as two parallel resistances !! shouldn't the current through c be 1.5 as well!!
That's what I thought as well. Even my science teacher said 1.5A :P
my first answer was 1.5 but i got it right eventually
I think most of you who are getting 1.5 amps as an answer are forgetting a vital formula that was essential in solving this problem. There is a relationship between length of wire and resistance. This factor will change 1.5 amps into 3 amps. The formula is R= (P * L)/A. P is resistance of the wire, L is the length of the wire, and A is the perpendicular-cross sectional area of the wire.
if it takes shape into circle then why it's resitance no change as R is proportional to L
Read allaboutcircuits.com
A battery is connected to the Point A and Point B of a homogenous wire. Therefore, both flow together and it is bent into a circle shape so both of the wires are at the same length. Then find Point C I = 1.5A Amps of Point C = Point A + Point B Amps of Point C = 1.5 + 1.5 = 3 Amps
No it has only 1 wire but both have same length
Don't forget to mention about using ohms law.
This one is extremely simple.
Alright so we know I = R V (ohm's law), and the internal resistance of the wire can be given as R = * A p × L , where * V is the voltage, I is the current, R is the resistance, L is the length of the conducting wire, p is the resistivity of the conducting wire, and A is the perpendicular-cross sectional area of the wire (imagine the wire being a long cylinder, and A being the area of the base circle).
From these, we can plug in the resistance formula and achieve this...
*I ∝ * L 1
which is a bit counter-intuitive, but hey, you've probably already been warned about this.
This means that if the length of wire from one battery to another is shortened by a factor of 2 1 , the current running through will raise by a factor of 2 .
This gives us our answer, 2 × 1 . 5 A m p s = 3 . 0 A m p s
This answer, of course, is assuming that the bottom half of the circle has become a separate circuit from the top half.
Let the resistance of the wire be R . The first thing to remember is that the resistance is directly proportional to the length of the wire . So, in the second case, as the semicircular piece of the wire between A and B is exactly half the length of the original wire, the resistance of each piece will be 2 R . As the two pieces of the wires are connected in parallel, the voltage across the terminals will be the same, say V . So, by Ohm's Law, V = I ′ 2 R = I R . Since the resistance is halved, the current is doubled so that V remains the same. Therefore, I ′ = 2 I = 3 A
Correct solution good work!!
Its current in parallel.
current flows equally from both sides.
and let the current flowing from c is x
1/AB = 1/x + 1/x
1/1.5 = 2/x
x = 2 x 1.5
x=3
Assume the wire's resistance is 2 ohms. Then the voltage of AB is 3 volts by ohm's law which is V = IR. When the same wire is bent into a circle, the distance of AB is half of the length it used to be therefore the resistance also halfs. Now each branch is 1 ohm and the voltage drop across each branch is still 3 volts by using the voltage divider formula. Subsistuting these values in the ohms law equation, we solve for I = current. 3= Current * 1. Now its simple to deduce that current flowing across point C is 3 amps.