Cone and sphere.
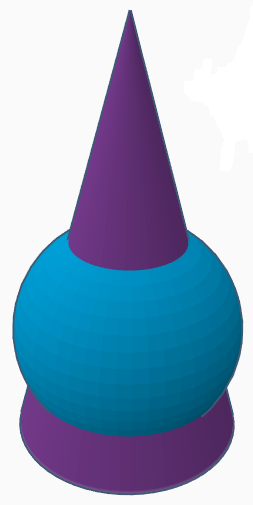
The sphere and the base of the cone each have radius . The sphere is tangent to the base of the cone at its center. Their intersections are two circles. If the larger circle has three times the area of the smaller circle, find the height of the cone.
The answer can be written as where are integers and b is square-free. Answer as the value of .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This can be done in two-dimensions, the sphere becomes a circle, the cone becomes a triangle and the radii of the circles become line segments.
To solve with a graph, let the circle be x 2 + y 2 = 1 and choose the line with positive slope, it contains ( − 1 , − 1 ) and ( 0 , h − 1 ) where h is the height of the cone so its equation is y = h x + h − 1 . The point of intersection A and B need to satisfy ( x B x A ) = 3
Substituting the line into the circle and solving for x gives
x 2 + ( h x + h − 1 ) 2 = 1
( h 2 + 1 ) x 2 + ( 2 h 2 − 2 h ) x + ( h 2 − 2 h ) = 0
x = h 2 + 1 h − h 2 ± 2 h Of the solutions, the one with the " + " is the smaller so dividing to get the required ratio gives
h − h 2 + 2 h h − h 2 − 2 h = 3
This can lead to a cubic whose only real solution is h = 2 + 3
so a + b + c = 2 + 3 + 1 = 6