Cone, Sphere, and Cylinder experiment
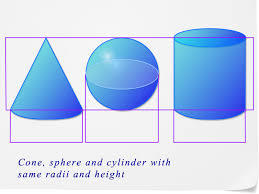
A student did an experiment using a cone, a sphere, and a cylinder each having the same radius and height. He started with the cylinder full of liquid and then poured it into the cone until the cone was full. Then, he began pouring the remaining liquid from the cylinder into the sphere. What was the result which he observed?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The volume of water we have is the volume of the cylinder of a radius R and height 2 R , namely:
V c y l i n e r = π R 2 ⋅ 2 R = 2 π R 3
The volume which is left after we pour the water into cone of radius R and height 2 R is:
V c y l i n d e r − V c o n e = 2 π R 3 − 3 1 π R 2 ⋅ 2 R = 2 π R 3 − 3 2 π R 3 = 3 4 π R 3
....which of course is the total volume of a sphere! We have no water left.
Excellent!
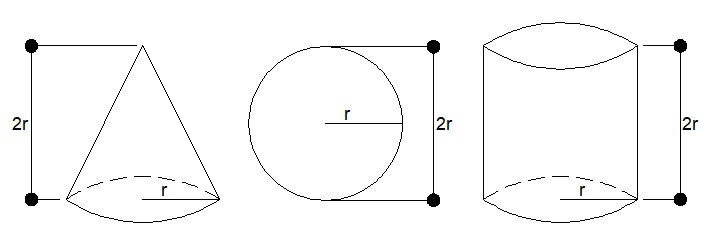 One way to do this is to compare the volumes of the cylinder against the sum of the volumes of the sphere and cone. The volume of the cylinder is
π
r
2
(
2
r
)
=
2
π
r
3
. The sum of the volumes of the sphere and the cone is
3
4
π
r
3
+
3
1
π
r
2
(
2
r
)
=
3
4
π
r
3
+
3
2
π
r
3
=
2
π
r
3
. Since the volumes are equal the desired answer is
There was exactly enough liquid left to fill the sphere
One way to do this is to compare the volumes of the cylinder against the sum of the volumes of the sphere and cone. The volume of the cylinder is
π
r
2
(
2
r
)
=
2
π
r
3
. The sum of the volumes of the sphere and the cone is
3
4
π
r
3
+
3
1
π
r
2
(
2
r
)
=
3
4
π
r
3
+
3
2
π
r
3
=
2
π
r
3
. Since the volumes are equal the desired answer is
There was exactly enough liquid left to fill the sphere
The volume of the cylinder is V c y l i n d e r = π r 2 h , however, h = 2 r . So it becomes V c y l i n d e r = 2 π r 3 .
The volume of the cone is V c o n e = 3 1 π r 2 h , however, h = 2 r . So it becomes V c o n e = 3 2 π r 3 .
After pouring some liquid from the cylinder to the cone (until the cone is full), the remaining volume of liquid is 2 π r 3 − 3 2 π r 3 = 3 4 π r 3 , which is exactly the volume of the sphere.
Conclusion: There was exactly enough liquid left to fill the sphere