Cone Surface Dynamics

The equations of motion can be easily derived using the Lagrangian approach. Let:

$m =1$

The kinetic energy of the particle reads:

$T = \frac{1}{2}\left(2 \dot{r}^2 +r^2 \dot{\theta}^2\right)$ $V = 10r$

Lagrange's equations read:

$\frac{d}{dt}\left(\frac{\partial T}{\partial \dot{r}}\right) - \frac{\partial T}{\partial r} + \frac{\partial V}{\partial r}=0$ $\implies \ddot{r} = \frac{r \dot{\theta}^2}{2} - 5 \ \dots (1)$

$\frac{d}{dt}\left(\frac{\partial T}{\partial \dot{\theta}}\right) - \frac{\partial T}{\partial \theta} + \frac{\partial V}{\partial \theta}=0$ $\frac{d}{dt}\left(\frac{\partial T}{\partial \dot{\theta}}\right)=0$ $r^2 \dot{\theta} = K$

Applying initial conditions to the above equation gives:

$r^2 \dot{\theta} = 10 \ \dots (2)$

Replacing (2) in (1) gives:

$\ddot{r} = \frac{50}{r^3} - 5$ $r^2 \dot{\theta} = 10$

Solving the above numerically gives the required result. As for the trajectory, the particle seems to be confined to a 'bucket' as seen in the following figures:

Upto $t=200$

Upto $t =100$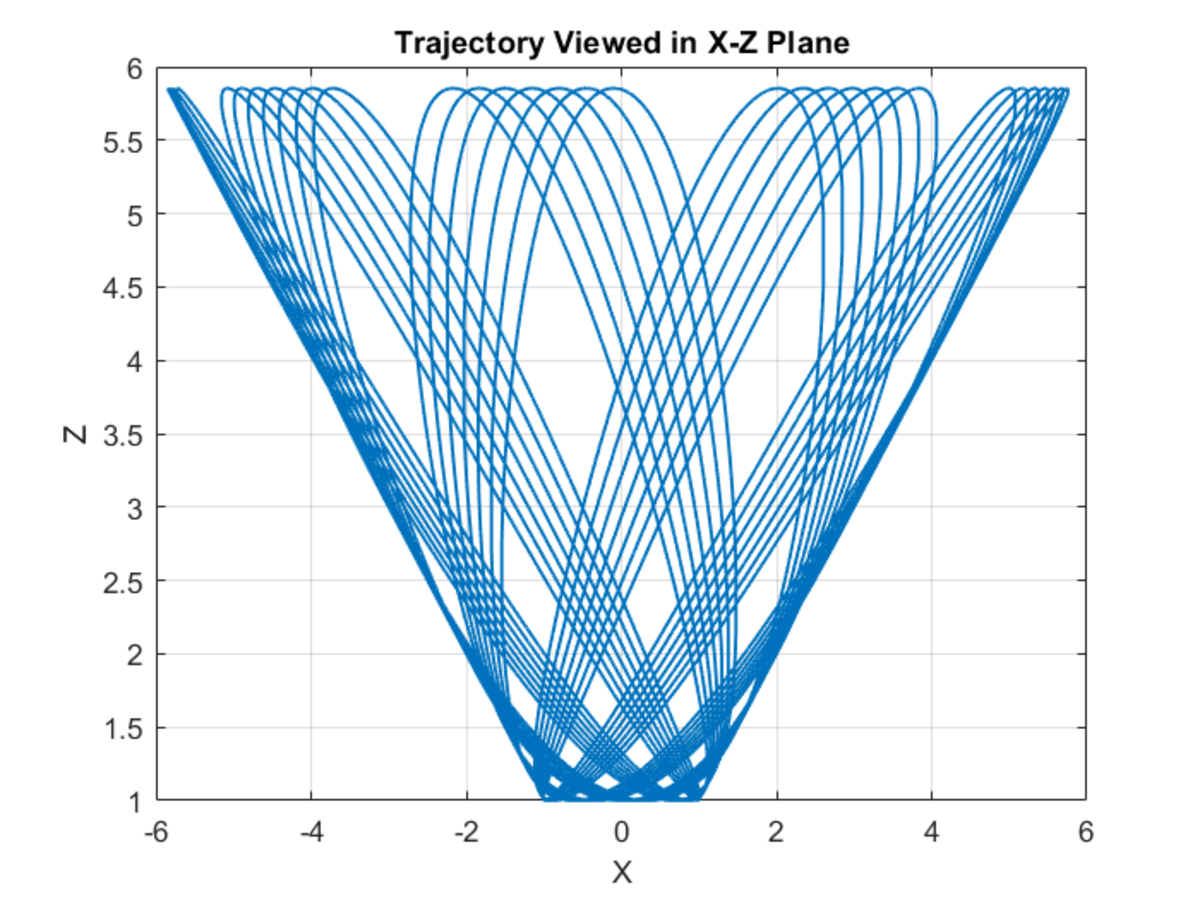

---

The solution was also attempted analytically and I made some headway but could not proceed beyond a point.

---

Derivation using Newton's laws:

Consider the particle to be on any point on the given conical surface.

$x = r \cos{\theta}$ $y = r \sin{\theta}$ $z = r$

Now, as the particle slides on the conical surface. It experiences the following forces:

• Gravity along the negative Z-direction
• Reaction force as the particle is in contact with the surface. Note that the reaction force is always normal to the surface.

The equation of the cone can easily be derived by seeing that:

$x^2 + y^2 = z^2$ $\Phi = x^2 + y^2 - z^2 = 0$

A vector normal to this surface can be computed as such:

$\nabla \Phi = \vec{n} = \left[\begin{matrix} 2x \\ 2y \\ -2z \end{matrix}\right]$

The corresponding unit vector is:

$\hat{n} = \frac{1}{\sqrt{x^2+y^2+z^2}}\left[\begin{matrix} x \\ y \\ -z \end{matrix}\right]$

Substituting $x$ , $y$ and $z$ gives:

$\hat{n} = \frac{1}{\sqrt{2}}\left[\begin{matrix} \cos{\theta} \\ \sin{\theta} \\ -1 \end{matrix}\right]$

Now, let the reaction force be $N$ . Applying Newton's second law:

$m \left[\begin{matrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{matrix}\right] = \left[\begin{matrix} 0\\ 0 \\ -mg\end{matrix}\right] + \frac{N}{\sqrt{2}}\left[\begin{matrix} \cos{\theta} \\ \sin{\theta} \\ -1 \end{matrix}\right]$

Let:

$\frac{N}{\sqrt{2}} = P$

The equations of motion are:

$m \left[\begin{matrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{matrix}\right] = \left[\begin{matrix} 0\\ 0 \\ -mg\end{matrix}\right] +P\left[\begin{matrix} \cos{\theta} \\ \sin{\theta} \\ -1 \end{matrix}\right]$

Now:

$m\ddot{z} = \ddot{r}$

$\ddot{r} = -g - P$ $\implies P = -g - \ddot{r}$

Replacing $P$ in the equations for $\ddot{x}$ and $\ddot{y}$ and and also writing $\ddot{x}$ and $\ddot{y}$ in terms of $r$ , $\theta$ , $\dot{r}$ , $\dot{\theta}$ , $\ddot{r}$ , $\ddot{\theta}$ gives us two massive equations. Solving those equations for $\ddot{r}$ , $\ddot{\theta}$ finally gives:

$\ddot{r} = \frac{r \dot{\theta}^2}{2} - \frac{g}{2}$ $\ddot{\theta} = -\frac{2 \dot{r} \dot{\theta}}{r}$