Factorial Sum!
1 ⋅ 1 ! + 2 ⋅ 2 ! + 3 ⋅ 3 ! + ⋯ + 2 5 ⋅ 2 5 ! = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
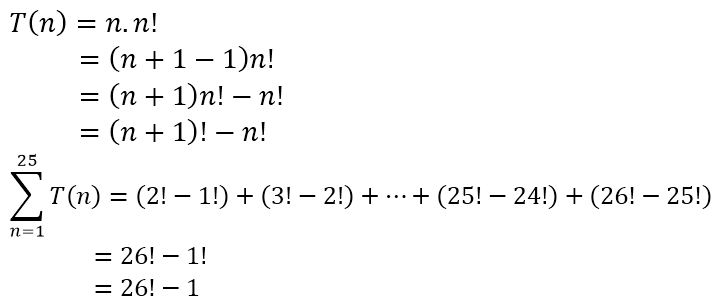
I am best at maths in the world. I know what 1+1 is .It is 2
Can be written as (2-1) 1! + (3-1) 2! + ...... (25-1) 24! + (26-1) 25! Further, it simplifies to 2!-1!+3!-2!+4!-3!+.....25!-24!+26!-25! which gives us 26!-1 as the correct answer.
can u elaborate neha gupta
Log in to reply
Create a difference form In RHS rightmost last term 26!-25!+25!-24!.....2!-1!=and
That's gorgeous, Neha! Thank you. Like a telescoping series.
How did you make the first analysis of (2-1) as the correct simplification?
Neha in which class u are
We can prove by induction that, more generally:
∑ k = 1 n k ⋅ k ! = ( n + 1 ) ! − 1
for all positive integers n .
For n = 1 we get 1 = 2 ! − 1 , which is correct.
Suppose now that the statement holds for certain n ∈ N . Then we have:
∑ k = 1 n + 1 k ⋅ k ! = ( n + 1 ) ! − 1 + ( n + 1 ) ( n + 1 ) ! = ( n + 2 ) ( n + 1 ) ! − 1 = ( n + 2 ) ! − 1 .
Hence the statement holds for all natural n . Plugging in n = 2 5 , we obtain:
1 ⋅ 1 ! + 2 ⋅ 2 ! + … + 2 5 ⋅ 2 5 ! = 2 6 ! − 1 .
Moderator note:
Good. There's another way to obtain this. Hint: k = k + 1 − 1 .
Can you interpret this number? If we arrange all possible permutation of alphabets in ascending order (from A smallest to Z largest), then what position would { Z , Y , X , W , V , … , C , B , A } be?
A nice alternate solution is to write k = k + 1 − 1 , so k ⋅ k ! = ( k + 1 − 1 ) ⋅ k ! = ( k + 1 ) ⋅ k ! − k ! = ( k + 1 ) ! − k ! .
Then, the terms of the sum cancel out, and we are left with ( 2 5 + 1 ) ! − 1 ! = 2 6 ! − 1 . This approach is known as a Telescoping Series Sum .
for Tijmen Veltman solution, plugging n=25 gets you 27!-1
Log in to reply
noasdnfoksadjfasdf ]
Let S = 1 ⋅ 1 ! + 2 ⋅ 2 ! + 3 ⋅ 3 ! + . . . 2 5 ⋅ 2 5 ! and let A = 1 ! + 2 ! + 3 ! + 4 ! + . . . 2 5 ! . Then,
S + A = ( 1 ⋅ 1 ! + 1 ! ) + ( 2 ⋅ 2 ! + 2 ! ) + ( 3 ⋅ 3 ! + 3 ! ) + . . . ( 2 5 ⋅ 2 5 ! + 2 5 ! ) Or, S + A = 2 ! + 3 ! + 4 ! + . . . 2 6 ! = A − 1 + 2 6 !
This gives,
S + A = 2 6 ! + A − 1
Or, S = 2 6 ! − 1 .
the LHS can be written as (1-0).1!+(3-1).2!+(4-1).3!+.......+(26-1).25! on simplification we will get 1!+3!-2!+4!-3!+5!-4!...........+26!-25! = 1!-2!+3!-3!+4!-4!+5!-5!+..........+25!-25!+26! =26!-2+1 = 26!-1
k*k!=(k+1)!-k! so all of the terms cancels out except of -1! and 26!, Which gives us 26!-1!
nth term = n.n! In place of first n put n+1-1 and multiply. nth term becomes n+1! - n!.
Can be proven with a strong induction: ( n + 1 ) ! − 1 + n + 1 ( n + 1 ) ! = ( n + 1 ) ! ( n + 1 + 1 ) − 1 = ( n + 2 ) ! − 1
I did something totally different from all the other comments here.
what i did is that i found out what the answer of 1 1!+2 2!+3 3!+4 4!+5*5! would be.
i basically then solved 1+4+18+36+600, and got 719.
i then noticed that my answer is just 1 number away from 6!, and thus, my answer = 6!-1.
I applied this for the full question, and immediately saw that the correct answer is 26!-1.
I have been using this technique for several problems here, and it always works. reduce the problem to smaller numbers which are easier to deal with, calculate them, and then predict what the answer is going to be. For some problems you will need more calculations to predict the answer even better.
may not be the best "mathematical way", but this technique could be useful when stuck at questions in competitive maths.
let 1·1!+2·2!+3·3!+.........+25·25! = x
Add 1!+2!+3!+.......+25! on both sides
we get,
2·1!+3·2!+4·3!+...........+26·25! = x + 1!+2!+3!+..........+25!
2! + 3! + 4! + .........+25! + 26! = x + 1! + 2! + 3! +.......... +25!
26! = x + 1!
Thus, x=26! - 1! = 26! -1
or,
1·1!+2·2!+3·3!+.........+25·25! = x = 26! - 1
It's a formula. The proof is simple. Replace n by n+1-1 in n.n! to get n+1!-n! Then simply add the terms to get n+1!-1.Therefore, the answer 26!-1