Confusing question. No way out
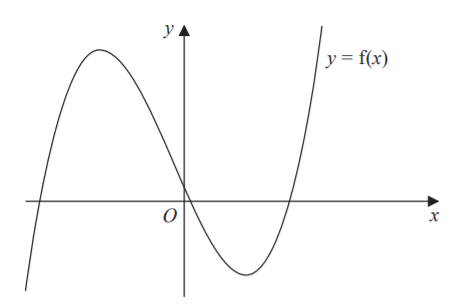
This figure shows the graph of y = f ( x ) = 2 x 3 + 2 3 x 2 − 1 8 x + 3 . Given that the equation f ( x ) = k , where k is a constant, has only one real root, find the set of values for k .
The answer can be of the form a < k < b or k < a ∪ k > b , where a and b are real numbers, submit a + b .
The answer is 15.125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The alternative way of getting a and b is as follows. First, we can insert the expression for r 1 in terms of r 2 into (3):
− ( − 4 3 − 2 r 2 ) r 2 2 = 2 3 − k k = 3 − 2 3 r 2 2 − 4 r 2 3
Substituting the values for r 2 and noting again that the greater value of r 2 corresponds with a and the lower value corresponds with b ,
a = 3 − 2 3 ( 2 3 ) 2 − 4 ( 2 3 ) 3 = − 8 1 1 1 b = 3 − 2 3 ( − 2 ) 2 − 4 ( − 2 ) 3 = 2 9
The two methods seem about equally fast.
The equation g ( x ) = k (where k is a constant) represents a horizontal line. So for f ( x ) = k to have only one real root, the horizontal line must cross f ( x ) only once, which can only occur below Q , the local minimum of f ( x ) (so that k < a ), or above P , the local maximum of f ( x ) (so that k > b ).
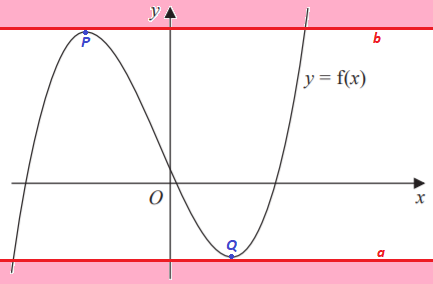
The local minimum and maximum of f ( x ) can be found by setting its derivative equal to zero and solving, so f ′ ( x ) = 6 x 2 + 3 x − 1 8 = 0 which solves to x = 2 3 and x = − 2 , so that Q is ( 2 3 , − 8 1 1 1 ) and P is ( − 2 , 2 9 ) . Therefore, a = − 8 1 1 1 and b = 2 9 , which means a + b = 8 1 2 1 = 1 5 . 1 2 5 .
To solve this we can use the most basic concept from calculus : the derivative
The function given is
2
x
3
+
2
3
x
2
+
−
1
8
x
+
3
, so it follows that the derivative is
6
x
2
+
3
x
−
1
8
.
To find the points of slope 0 we must solve
2
x
2
+
x
−
6
=
0
which is (2x-3)(x+2) = 0 so the answers are 1.5 and -2
Now we can evaluate y for these values and then shift the function by manipulating k.
The coordinates are (1.5, -13.875) and (-2,29). Thus we have the range of functions with 3 real roots as -13.875 < k < 29 because the points are on different sides of the x axis. Thus the range we are looking for is k >29 or k< -13.875 so 29 - 13.875 =
15.125
The derivative of the function is zero at ( − 2 , 2 9 ) and ( 1 . 5 , − 1 3 . 8 7 5 ) .
1 9 + ( − 1 3 . 8 7 5 ) = 1 5 . 1 2 5
I would change this to a calculus problem.
Ok I have changed it to calculus. Thanks.
To solve without calculus...
f has a local minimum a and a local maximum b , between which any horizontal line will intersect f three times. Below a and above b , a horizontal line will intersect the curve only once; these are the two regions in which k can exist. The curve intersects the horizontal line y = k when f ( x ) = k . Thus,
2 x 3 + 2 3 x 2 − 1 8 x + 3 = k x 3 + 4 3 x 2 − 9 x + 2 3 − k = 0 .
To find a and b , we will utilize the remaining case, in which k is precisely a or b . Now, the horizontal line y = k intersects f twice , and one of the two intersections is tangent to the curve at the extremum, meaning it will account for a double instance of one of the roots when the two functions are equated. Thus, the left side side of the equation can be factored as ( x − r 1 ) ( x − r 2 ) 2 , where r 1 and r 2 are the roots of the new cubic expression involving k . Expanding, we have
x 3 − ( r 1 + 2 r 2 ) x 2 + ( 2 r 1 r 2 + r 2 2 ) x − r 1 r 2 2 = x 3 + 4 3 x 2 − 9 x + 2 3 − k .
Using the property of such polynomial equations that the coefficient of each term on the left side must equal the coefficient of the corresponding term on the right side, we now have the following system of three equations with three unknowns:
From (1), we find that r 1 = − 4 3 − 2 r 2 . Then, from (2), substituting the new expression for r 1 in terms of r 2 and rearranging gives us the quadratic
r 2 2 + 2 1 r 2 − 3 = 0 ,
which has solutions r 2 = 4 − 1 ± 7 . We could continue solving the system, but we already have what we need because r 2 , being the root that occurs twice, is in fact the x -coordinate of the extremum. Therefore, a and b are the values of f ( x ) for the greater and lower values of r 2 , respectively:
a = f ( 4 − 1 + 7 ) = f ( 2 3 ) = − 8 1 1 1 b = f ( 4 − 1 − 7 ) = f ( − 2 ) = 2 9
Finally, a + b = 2 9 − 8 1 1 1 = 8 1 2 1 = 1 5 . 1 2 5 .