Congruency grows complex

We observe that $z_1\equiv z_2\pmod{2+i}$ if $z_1-z_2=(2+i)(a+bi)=a(2+i)+b(-1+2i)$ , meaning that $z_1-z_2$ is an integer linear combination of $2+i$ and $-1+2i$ . Consider the lattice spanned by $2+i$ and $-1+2i$ ; as a fundamental domain, choose the square with its vertices at $0, 2+i, -1+2i,$ and $1+3i.$ As representatives of our congruency classes, we can choose the four points in this fundamental domain, $i, 2i, 1+i$ and $1+2i$ and add one of the vertices of the square, 0, say, for a total of $\boxed{5}$ classes.

See the excellent figure in 展豪 張's solution.

(We could use Pick's Theorem to count the points in the fundamental domain without actually finding them.)

This approach shows, more generally, that there are $a^2+b^2$ congruency classes modulo $a+bi$ .

Since $N(2+i) = |2+i|^2 = 5$ is prime, $2+i$ is an irreducible element in the Euclidean domain $\mathbb{Z}[i]$ . Thus the ideal $\langle 2+i \rangle$ is a prime, so maximal, ideal in $\mathbb{Z}[i]$ , and hence the quotient ring $\mathbb{Z}[i]/\langle 2+i\rangle$ is a field.

Since $a + bi \, =\, (a - 2b) + b(2+i)$ for any $a,b \in \mathbb{Z}$ , we deduce that every Gaussian integer is congruent to a real integer in this field, so that $\mathbb{Z}[i]/\langle 2+i\rangle \; = \; \big\{ a + \langle 2+i \rangle \,\big|\, a \in \mathbb{Z} \big\} \;.$ Since, moreover, $5 \,=\, (2+i)(2-i)$ , we see that $5 \equiv 0$ , and hence that $\mathbb{Z}[i]/\langle 2+i\rangle \; = \; \big\{ a + \langle 2+i \rangle \,\big|\, a = 0,1,2,3,4 \big\} \;.$ If $0 \le a \le b \le 4$ were such that $a \equiv b$ , then $b-a = (2+i)w$ for some Gaussian integer $w$ , and hence $(b-a)^2 = N(b-a) = 5N(w)$ is an ordinary multiple of $5$ . Since $1^2,2^2,3^2,4^2$ are not multiples of $5$ , we deduce that $a=b$ . Thus the congruence classes $a + \langle 2+i\rangle$ , for $a=0,1,2,3,4$ , are distinct, and hence the field $\mathbb{Z}[i]/\langle 2+i\rangle$ contains $\boxed{5}$ elements.

Since $\mathbb{Z}[i]/\langle 2+i\rangle$ is a field, all but one (namely $4$ ) of the congruence classes are units. The congruence classes of $2$ and $3$ are mutual inverses, and the congruence classes of $1$ and $4$ are self-inverse.

My approach is graphical:
First I think of a line passing $0$ and $2+i$
Then I remember that $i$ , which is a Gaussian Integer, somehow 'represents' a rotation of $90$ degrees.
So I draw a line passing $0$ and $-1+2i$
Then I finish the square:

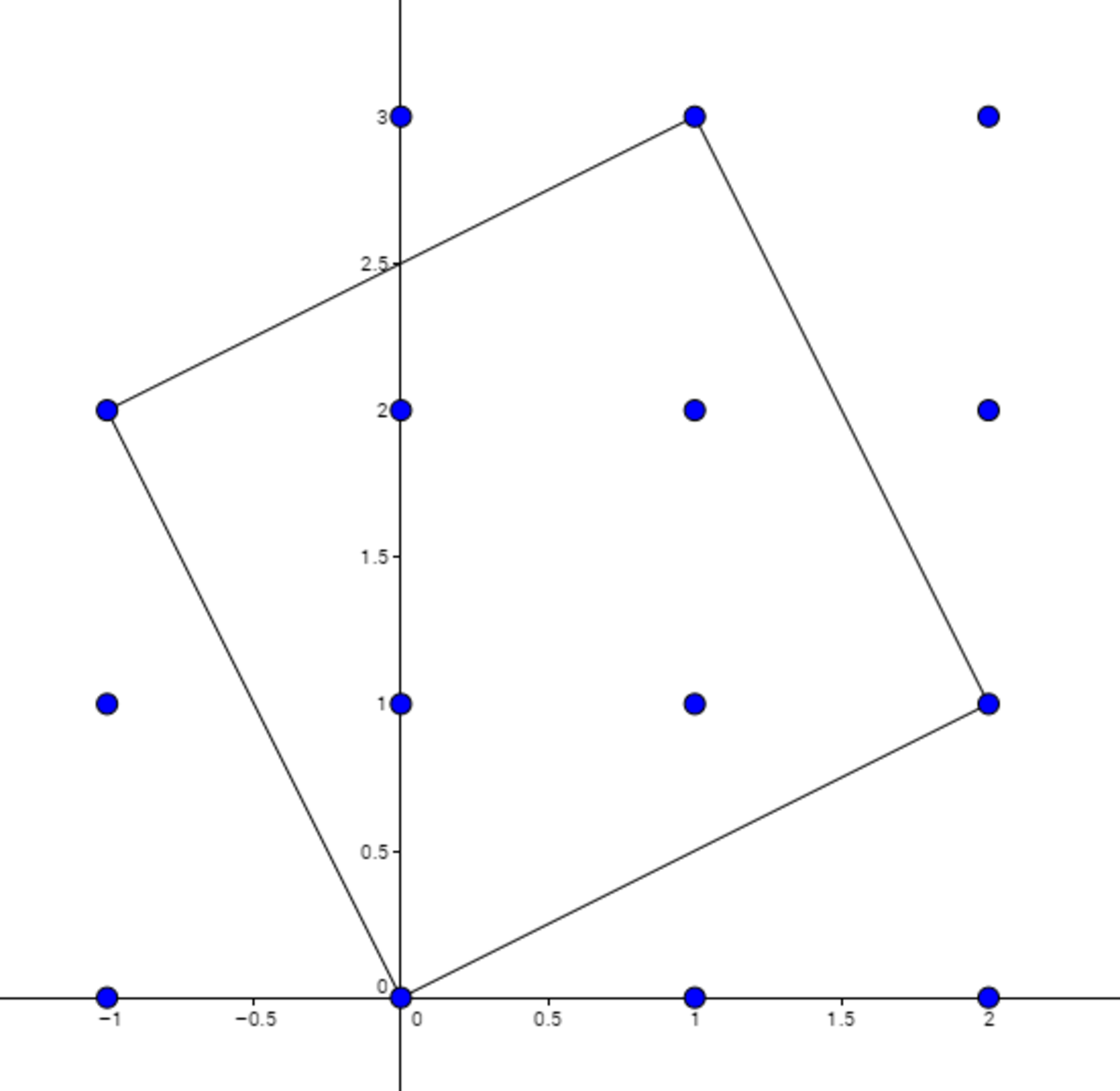
So there are $5$ congruency classes: the $4$ points inside, and $1$ vertex of the square.