Congruent AND Concurrent
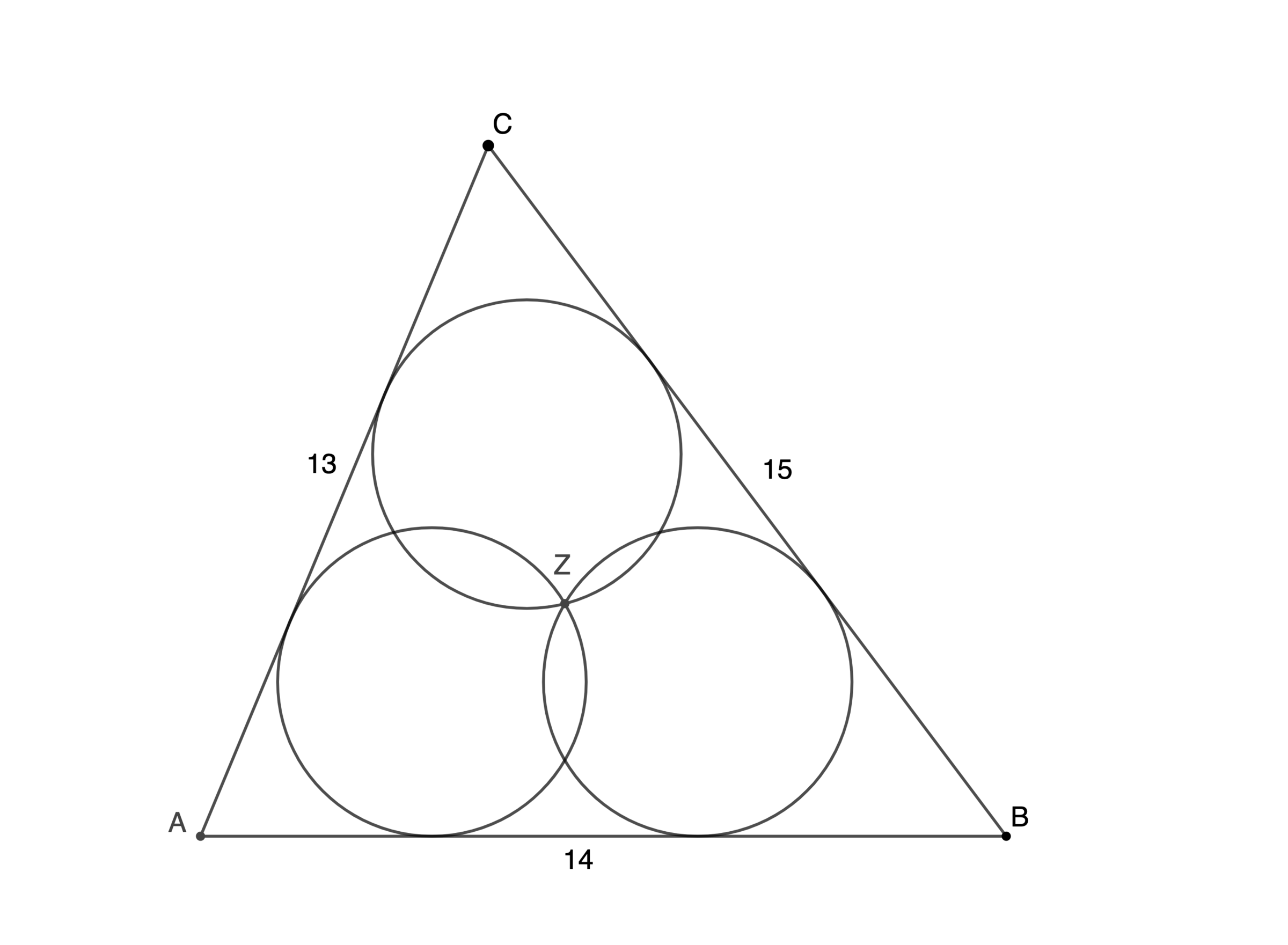
is a - - triangle in which three congruent circles are each tangent to two sides of the triangle and are concurrent at . What is their radius? Express it as , where and are coprime positive integers and submit .
The answer is 357.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let D , E , and F be the centers of the three congruent circles with radius r , and draw in and label the diagram as follows:
By Heron's formula, the area of △ A B C is A △ A B C = s ( s − a ) ( s − b ) ( s − c ) = 2 1 ( 2 1 − 1 3 ) ( 2 1 − 1 4 ) ( 2 1 − 1 5 ) = 8 4 .
Since each circle is tangent to the sides of △ A B C , the centers D , E , and F are on the angle bisectors of A , B , and C .
A 1 3 - 1 4 - 1 5 triangle is a 5 - 1 2 - 1 3 triangle combined with a 9 - 1 2 - 1 5 , so A G = D G cot ∠ D A G = r cot ( 2 1 ∠ C A B ) = r cot ( 2 1 cos − 1 ( 1 3 5 ) ) = 2 3 r and H B = E H cot ∠ E B H = r cot ( 2 1 ∠ A B C ) = r cot ( 2 1 cos − 1 ( 1 5 9 ) ) = 2 r , so that D E = G H = A B − A G − H B = 1 4 − 2 3 r − 2 r = 1 4 − 2 7 r .
Since the sides of △ D E F are parallel to the sides of △ A B C , the two triangles are similar, and have a side ratio of A B D E = 1 4 1 4 − 2 7 r = 1 − 4 1 r .
Since Z D = Z E = Z F = r , Z is the circumcenter of △ D E F , so 2 r = 2 A △ D E F D E ⋅ E F ⋅ D F = ( 1 − 4 1 r ) 2 A △ A B C ( 1 − 4 1 r ) A B ⋅ ( 1 − 4 1 r ) B C ⋅ ( 1 − 4 1 r ) A C = 8 4 1 4 ⋅ 1 5 ⋅ 1 3 ⋅ ( 1 − 4 1 r ) , and 2 r = 8 4 1 4 ⋅ 1 5 ⋅ 1 3 ⋅ ( 1 − 4 1 r ) solves to r = 9 7 2 6 0 .
Therefore, p = 2 6 0 , q = 9 7 , and p + q = 3 5 7 .