Congruent Incircles
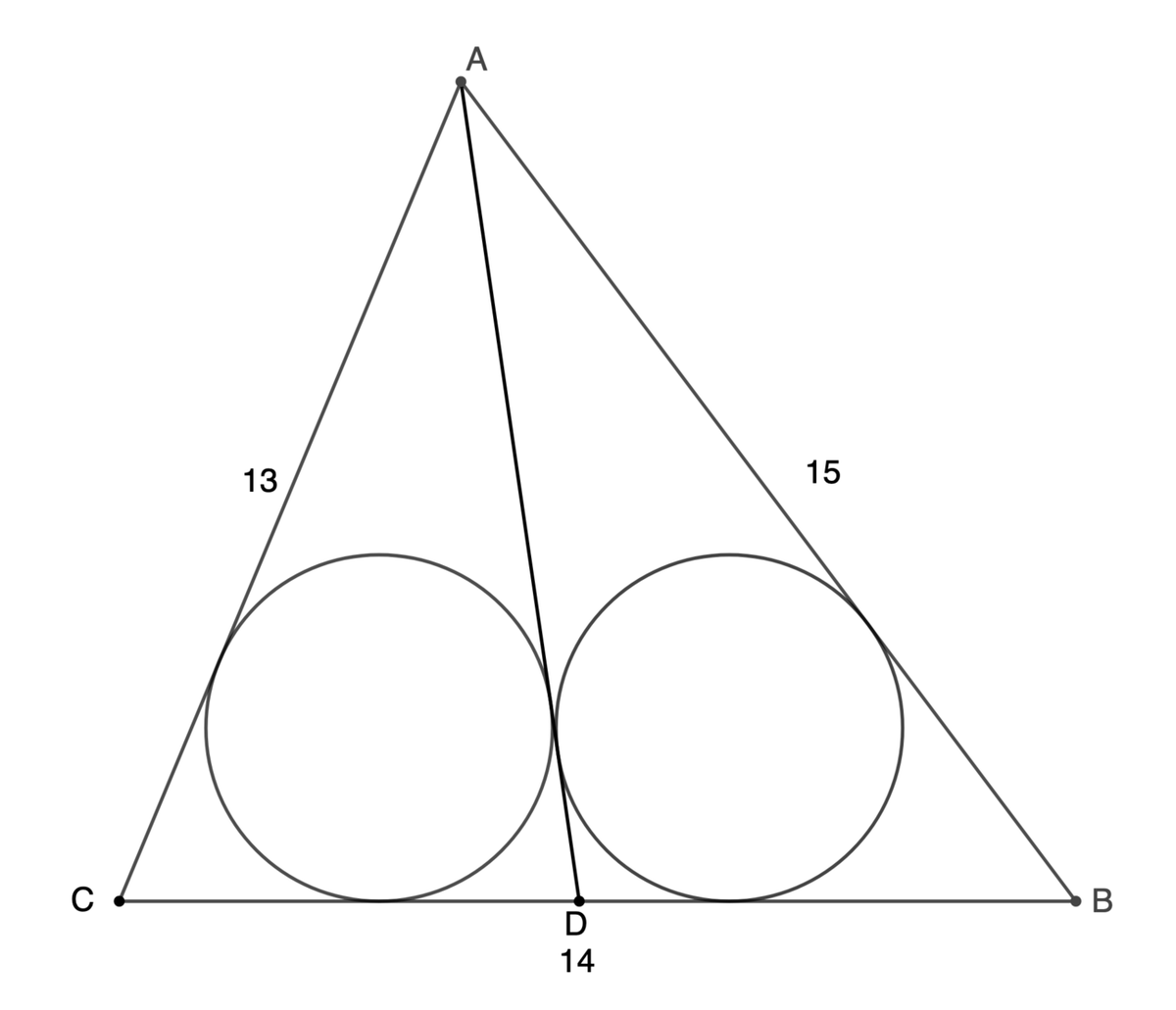
As shown in the figure △ A B C has side lengths 1 3 , 1 4 and 1 5 . A cevian A D is drawn such that two congruent incircles are inscribed. If the inradius is a + b c , where a , b and c are integers with c being square-free, submit a + b + c .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Confession: I couldn't prove this problem. I was unaware of its Sangaku origin (I thought it was original :)) and I am so glad you pointed this out. Also the "30 Sanagaku problems" paper looks fascinating. Thank you, @Thanos Petropoulos for such an informative solution.
Log in to reply
Thanks! I thought you had this Sangaku problem in mind when you came with "Congruent Incircles". And thanks for giving me the oportunity to mention this nice sangaku problem. PS. This time, your circles were not 'almost' congruent :)
I hadn't seen the formula in @Thanos Petropoulos ' solution before, but it simplifies things a lot.
If the common inradius is r , then the area of Δ A B C is 2 1 r ( 1 3 + 1 4 + 1 5 + 2 A D ) = r ( 2 1 + A D )
(using the fact that a triangle's area is its inradius times its semiperimeter in both A B D and A C D ). It's easy to verify (Heron's formula) that the area of A B C is 8 4 ; so r ( 2 1 + A D ) = 8 4
From the formula Thanos quotes, A D = 2 1 ⋅ 7 = 1 4 7
So r = 2 1 + 1 4 7 8 4 = 6 − 2 3
giving the answer 7 .
Excellent simplification!
The triangle A B C is a 5 , 1 2 , 1 3 triangle stuck to a 9 , 1 2 , 1 5 triangle, and hence has height 1 2 . Suppose that B D = x and A D = d . Then A C D has area 6 ( 1 4 − x ) and semiperimeter 2 1 ( 2 7 − x + d ) , while A B D has area 6 x and semiperimeter 2 1 ( 1 5 + x + d ) . Thus we deduce that 2 7 − x + d 1 2 ( 1 4 − x ) ( 1 4 − x ) ( 1 5 + x + d ) 2 1 0 − x + 1 4 d − x 2 − x d 2 1 0 − 2 8 x 7 ( 1 5 − 2 x ) = 1 5 + x + d 1 2 x = x ( 2 7 − x + d ) = 2 7 x − x 2 + x d = 2 ( x − 7 ) d = ( x − 7 ) d Thus we deduce that 7 < x < 7 2 1 and moreover, since cos B = 5 3 , we deduce that d 2 = 2 2 5 + x 2 − 1 8 x , so that 4 9 ( 1 5 − 2 x ) 2 1 9 6 x 2 − 2 9 4 0 x + 1 1 0 2 5 x 4 − 3 2 x 3 + 3 3 0 x 2 − 1 0 9 2 x x ( x − 1 4 ) ( x 2 − 1 8 x + 7 8 ) x ( x − 1 4 ) ( ( x − 9 ) 2 − 3 ) = ( x − 7 ) 2 ( x 2 − 1 8 x + 2 2 5 ) = x 4 − 3 2 x 3 + 5 2 6 x 2 − 4 0 3 2 x + 1 1 0 2 5 = 0 = 0 = 0 Since 7 < x < 7 2 1 , we deduce that x = 9 − 3 , so that d = 7 3 and hence the common inradius is 1 5 + x + d 1 2 x = 6 − 2 3 making the answer 6 + ( − 2 ) + 3 = 7 .
Nice work, I tried a similar approach but missed the cosine rule connection. Thank you.
By cosine rule , we have 1 5 2 = 1 3 2 + 1 4 2 − 2 ( 1 3 ) ( 1 4 ) cos C . ⟹ cos C = 1 3 5 . Then altitude of △ A B C is 1 3 sin C = 1 2 . Let the inradius be r , C D = x , and A D = ℓ . Then the areas of △ A C D and △ A D B are given by:
⎩ ⎪ ⎨ ⎪ ⎧ [ A C D ] = 2 1 3 + x + ℓ r = 2 1 2 x [ A D B ] = 2 2 9 − x + ℓ r = 2 1 2 ( 1 4 − x ) ⟹ ( 1 3 + x + ℓ ) r = 1 2 x ⟹ ( 2 9 − x + ℓ ) r = 1 2 ( 1 4 − x ) . . . ( 1 ) . . . ( 2 )
From ( 2 ) ( 1 ) :
2 9 − x + ℓ 1 3 + x + ℓ 1 8 2 + x + 1 4 ℓ − x 2 − x ℓ 9 1 − 1 4 x 9 1 − 1 4 x ⟹ x = 1 4 − x x = 2 9 x − x 2 + x ℓ = ( x − 7 ) ℓ = ( x − 7 ) ( x − 5 ) 2 + 1 2 2 = 5 + 3 Note that ℓ = ( x − 5 ) 2 + 1 2 2
From ( 2 ) − ( 1 ) :
( 1 6 − 2 x ) r ( 8 − x ) r ⟹ r = 1 2 ( 1 4 − 2 x ) = 1 2 ( 7 − x ) = 8 − x 1 2 ( 7 − x ) = 8 − 5 − 3 1 2 ( 7 − 5 − 3 ) = 3 − 3 1 2 ( 2 − 3 ) = 6 1 2 ( 2 − 3 ) ( 3 + 3 ) = 2 ( 3 − 3 ) = 6 − 2 3
Therefore a + b + c = 6 − 2 + 3 = 7 .
In this solution we use the fact that, in the case where the two incircles are congruent, the following relation holds: A D = s ⋅ ( s − a ) ( 1 ) where a = B C and s is the semiperimeter of △ A B C .
This is problem 2.2.5 in Fukagawa, Hidetoshi, and Dan Pedhoe. 1989, Japanese temple geometry problems, Winnipeg: Charles Babbage Research Centre. In this book no solution is given, but you can find one here (problem 8).
In our triangle we have s = 2 1 3 + 1 4 + 1 5 = 2 1 .
Using formula ( 1 ) , we get A D = 2 1 ⋅ 7 = 7 3 .
Let C D = x . Then, D B = 1 4 − x and by Stewart's Theorem on △ A B C for the cevian A D we have
C D ⋅ A B 2 + D B ⋅ A C 2 = B C ⋅ ( A D 2 + C D ⋅ D B ) ⇒ x ⋅ 1 5 2 + ( 1 4 − x ) ⋅ 1 3 2 = 1 4 ⋅ [ ( 7 3 ) 2 + x ⋅ ( 1 4 − x ) ] which solves to x = 5 + 3 or x = 5 − 3
Case 1 : x = 5 + 3
Denoting by s 1 and s 2 the semiperimeters of △ A C D and △ A B D respectively, we have s 1 = 2 1 3 + ( 5 + 3 ) + 7 3 = 4 3 + 9 and s 2 = 2 1 5 + [ 1 4 − ( 5 + 3 ) ] + 7 3 = 3 3 + 1 2 By Heron’s folmula [ A C D ] = ( 4 3 + 9 ) ( 4 3 − 4 ) ( 3 3 + 4 ) ( 9 − 3 3 ) = 3 0 + 6 3 and [ A B D ] = ( 3 3 + 1 2 ) ( 1 2 − 4 3 ) ( 4 3 + 3 ) ( 3 3 − 3 ) = 5 4 − 6 3 For the radii r 1 and r 2 of △ A C D and △ A B D respectively, we have
r 1 = s 1 [ A C D ] = 9 + 4 3 3 0 + 6 3 = 6 − 2 3 and r 2 = s 2 [ A B D ] = 1 2 + 3 3 5 4 − 6 3 = 6 − 2 3 We notice that r 1 = r 2 .
Case 2 : x = 5 − 3
Working the same way we find that r 1 = r 2 , hence this value is rejected.
To conclude, the common radius of the two circles is r = 6 − 2 3 .
For the answer, a + b + c = 6 − 2 + 3 = 7 .