Congruent parts
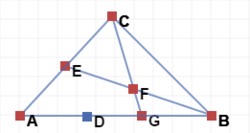 In triangle
A
B
C
above, if
A
E
=
E
C
and
A
D
=
D
G
=
G
B
, find
F
G
C
F
. If you've come to the conclusion that the value cannot be derived, type in 0.
In triangle
A
B
C
above, if
A
E
=
E
C
and
A
D
=
D
G
=
G
B
, find
F
G
C
F
. If you've come to the conclusion that the value cannot be derived, type in 0.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanx d bro.
How did you derive BG to -1 ?
Log in to reply
BG and AB are in opposite direction, so they must be of different sign.
Using a point mass system: M A = M C = 1 so M E = M A + M C = 2 Now A G : G B = M B : M A = 2 : 1 ∴ M A = 2 M G = M A + M B = 3 ∴ F G C F = M C M G = 3
What is point mass?
Log in to reply
You imagine that you have a mass at a point and that you want the weights to balance on the lines, in the same way that weights balance on levers. If you're still not sure, see the Barycentric Coordinates Wiki on Brilliant
Apply Menelaus' theorem
E A C E ⋅ B G A B ⋅ F C G F = − 1
1 1 ⋅ − 1 3 ⋅ F C G F = − 1
F G C F = 3