Congurent Triangles

Geometry Level 3

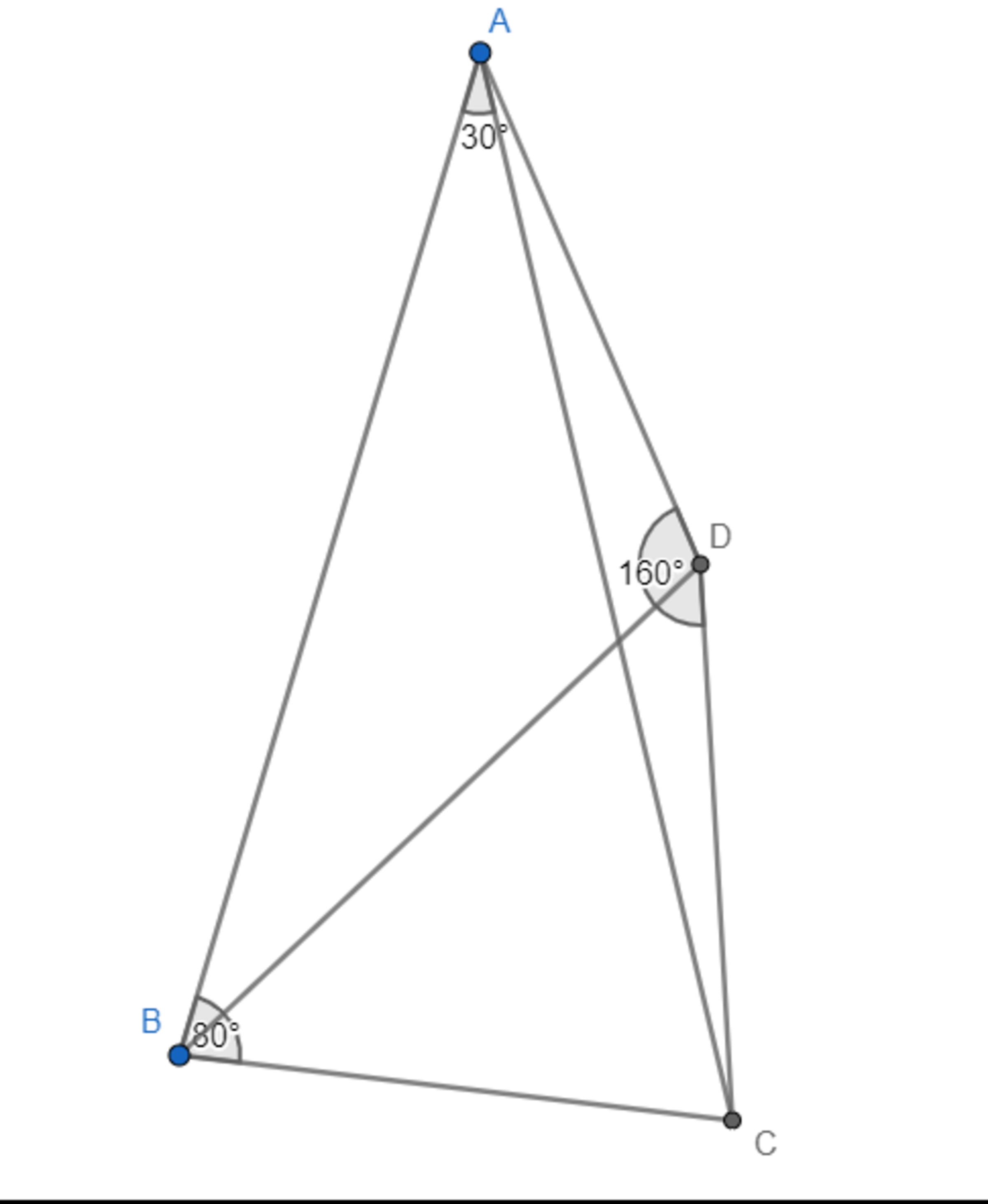Given a triangle $ABC$ whose angles $\widehat{BAC} = 30^o$ and $\widehat{ABC}=80^o$ .

Let there be a point D such that it isn't in the same half-plane of side AC with point B; and ADC is an isosceles triangle whose $\widehat{ADC} = 160^o$

Type your answer as the degree of the angle $\widehat {DBC}$ .

The answer is 50.

1 solution

Hongqi Wang
Dec 6, 2020

Let mirrored point of D with AC is O: $\\ OA = OC \\ \angle AOC = 160\degree = 2 \times 80\degree = 2\angle ABC\\$ So O is center of circumcircle circle of △ABC. And $OB = OC\\ \angle ACB = 180\degree - 30\degree - 80\degree = 70\degree \\ \angle OCB = \angle ACB - \frac {180\degree- 160\degree}{2} \\ = 70\degree - 10\degree = 60\degree\\$ i.e. △OBC is equilateral triangle and $\\ BC = OC = CD \\ \therefore \angle DBC = \frac{180\degree - (\angle ACB + 10\degree)}2 = 50\degree$

Congurent Triangles

The answer is 50.

1 solution

0 pending reports