Conics!
From a point A common tangents are drawn to the circle x 2 + y 2 = 2 and the parabola y 2 = 8 x . Find the area of the quadrilateral formed by the common tangents, the chord of contact of the circle and the chord of contact of the parabola.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
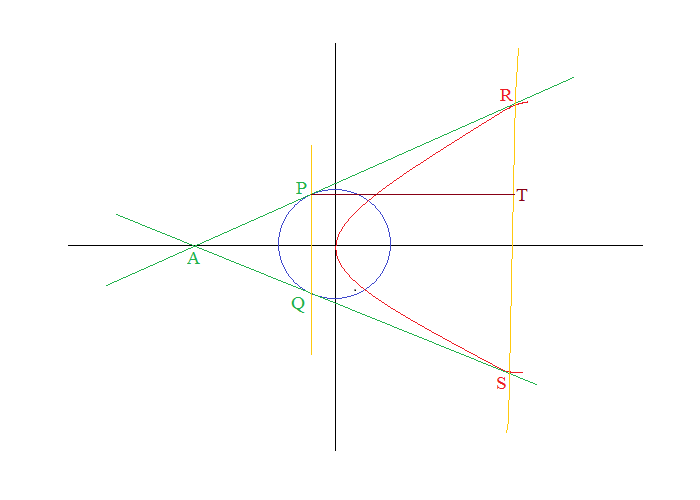 We need to find the area of the quadrilateral
P
Q
R
S
which is trapezium.
L
e
t
t
h
e
e
q
u
a
t
i
o
n
o
f
t
h
e
c
o
m
m
o
n
t
a
n
g
e
n
t
b
e
y
=
m
x
+
c
.
L
e
t
t
h
e
e
q
u
a
t
i
o
n
o
f
c
i
r
c
l
e
a
n
d
p
a
r
a
b
o
l
a
b
e
x
2
+
y
2
=
2
a
2
a
n
d
y
=
4
a
x
,
w
h
e
r
e
a
=
2
.
A
p
p
l
y
i
n
g
c
o
n
d
i
t
i
o
n
f
o
r
t
a
n
g
e
n
c
y
w
e
g
e
t
,
=
>
c
=
m
a
=
±
2
a
1
+
m
2
=
>
m
2
a
2
=
2
a
2
(
1
+
m
2
)
=
>
m
4
+
m
2
−
2
=
0
O
n
s
o
l
v
i
n
g
w
e
g
e
t
m
=
±
1
,
∴
e
q
u
a
t
i
o
n
o
f
t
a
n
g
e
n
t
s
w
i
l
l
b
e
,
=
>
y
=
x
+
a
a
n
d
y
=
−
x
−
a
N
o
w
w
e
c
a
n
f
i
n
d
t
h
e
i
n
t
e
r
s
e
c
t
i
o
n
p
o
i
n
t
s
o
f
t
a
n
g
e
n
t
a
n
d
c
i
r
c
l
e
a
n
d
t
a
n
g
e
n
t
a
n
d
p
a
r
a
b
o
l
a
.
∴
P
(
2
−
a
,
2
a
)
Q
(
2
−
a
,
2
−
a
)
R
(
a
,
2
a
)
S
(
a
,
−
2
a
)
A
r
e
a
o
f
q
u
a
d
r
i
l
a
t
e
r
a
l
P
Q
R
S
=
2
1
(
P
T
)
(
P
Q
+
R
S
)
=
>
a
r
e
a
=
2
1
(
a
+
2
a
)
(
a
+
4
a
)
=
>
a
r
e
a
=
2
1
×
2
3
a
×
5
a
=
>
a
r
e
a
=
4
1
5
a
2
P
u
t
t
i
n
g
a
=
2
,
a
r
e
a
=
4
1
5
×
4
=
1
5
We need to find the area of the quadrilateral
P
Q
R
S
which is trapezium.
L
e
t
t
h
e
e
q
u
a
t
i
o
n
o
f
t
h
e
c
o
m
m
o
n
t
a
n
g
e
n
t
b
e
y
=
m
x
+
c
.
L
e
t
t
h
e
e
q
u
a
t
i
o
n
o
f
c
i
r
c
l
e
a
n
d
p
a
r
a
b
o
l
a
b
e
x
2
+
y
2
=
2
a
2
a
n
d
y
=
4
a
x
,
w
h
e
r
e
a
=
2
.
A
p
p
l
y
i
n
g
c
o
n
d
i
t
i
o
n
f
o
r
t
a
n
g
e
n
c
y
w
e
g
e
t
,
=
>
c
=
m
a
=
±
2
a
1
+
m
2
=
>
m
2
a
2
=
2
a
2
(
1
+
m
2
)
=
>
m
4
+
m
2
−
2
=
0
O
n
s
o
l
v
i
n
g
w
e
g
e
t
m
=
±
1
,
∴
e
q
u
a
t
i
o
n
o
f
t
a
n
g
e
n
t
s
w
i
l
l
b
e
,
=
>
y
=
x
+
a
a
n
d
y
=
−
x
−
a
N
o
w
w
e
c
a
n
f
i
n
d
t
h
e
i
n
t
e
r
s
e
c
t
i
o
n
p
o
i
n
t
s
o
f
t
a
n
g
e
n
t
a
n
d
c
i
r
c
l
e
a
n
d
t
a
n
g
e
n
t
a
n
d
p
a
r
a
b
o
l
a
.
∴
P
(
2
−
a
,
2
a
)
Q
(
2
−
a
,
2
−
a
)
R
(
a
,
2
a
)
S
(
a
,
−
2
a
)
A
r
e
a
o
f
q
u
a
d
r
i
l
a
t
e
r
a
l
P
Q
R
S
=
2
1
(
P
T
)
(
P
Q
+
R
S
)
=
>
a
r
e
a
=
2
1
(
a
+
2
a
)
(
a
+
4
a
)
=
>
a
r
e
a
=
2
1
×
2
3
a
×
5
a
=
>
a
r
e
a
=
4
1
5
a
2
P
u
t
t
i
n
g
a
=
2
,
a
r
e
a
=
4
1
5
×
4
=
1
5
Nice solution :)
Did the same but this is brute force
Log in to reply
Yeah truly it's lengthy ......
I didnt used brute force. I am quite lazy and dont use it :)
I have seen this before, may be in IIT past papers.
Log in to reply
You are absolutely correct.This question was asked in IIT.
Very lengthy