Conjecture + Calculus = Conjectulus?
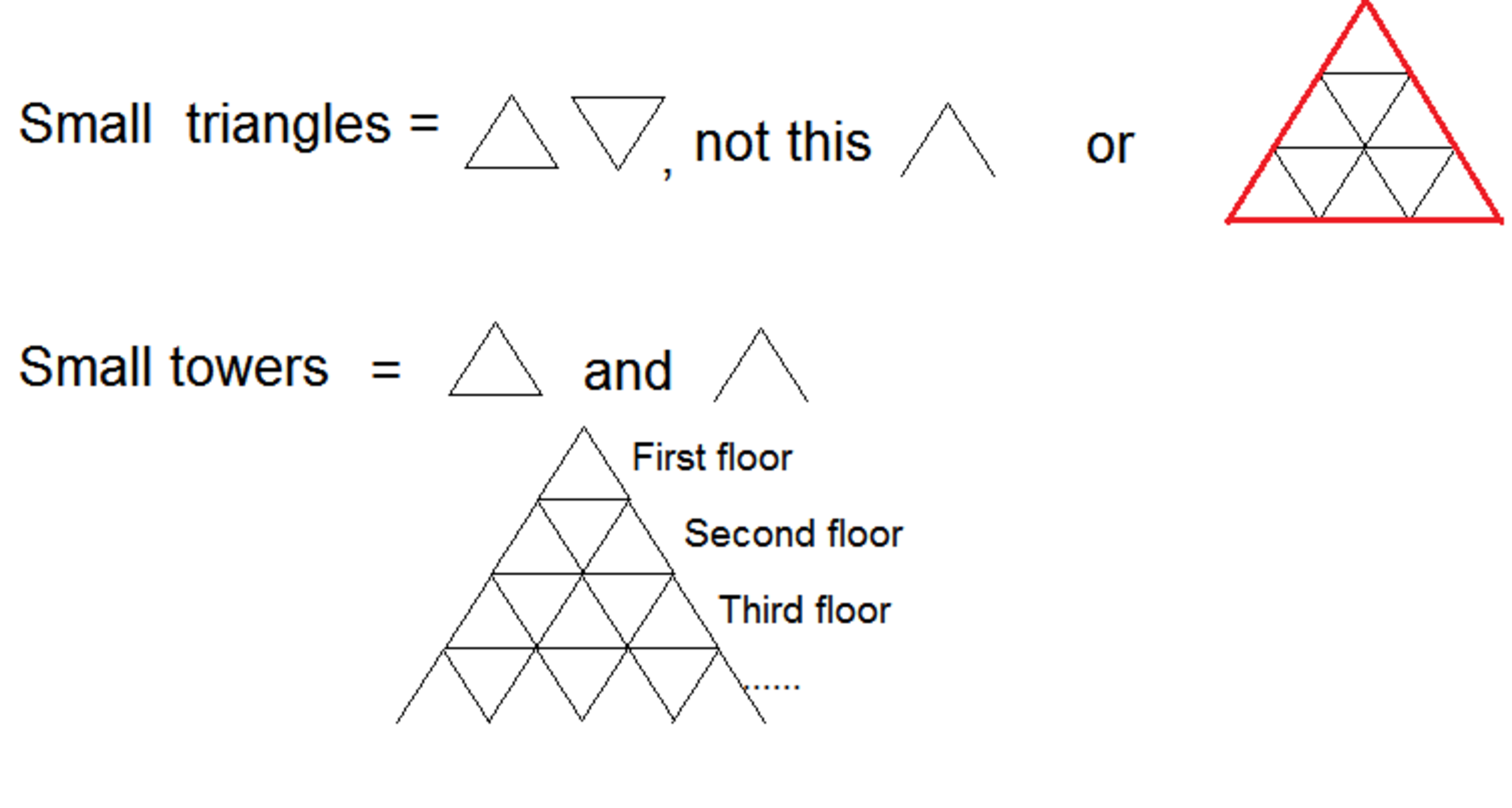
Have you ever took some playing cards and start to make a pyramid of them, like a house of cards? Well, Mohamed has already played it a lot of times. Here's the image of what I'm talking about:
Wikipedia.
So, Mohamed was very interesting about the way that the pyramid behaviors, first because it kinda looks like a growing tree, and second weather was possible to predict how the structure would looks like in a certainly quantity of cards and "floors". And then he start to make his conjecture about the pyramid, ending with success. Here it is what he got:
A formula to predict how many will have this pyramid;
A formula to predict how many will need to make the pyramid; and
A formula to predict how many of will have the pyramid.
All three formulas which obey the proportion of "How many floors" has the pyramid.
After that, satisfied with his result, he come back to imagine the growing of the pyramid like a tree does, in a constant process. With that in mind, he calculated the instantaneous derivative of the three functions.
Answer this: what is the value of the sum of the three instantaneous derivative when the tree pyramid has 68 "floors"?
Consider that all the cards are as I drew in the paint:
When calculating the derivative of the functions, consider to all real numbers.
*This is a original problem (I think...). In the case of ambiguity, just let me know so I can see if I can fix it. .
The answer is 408.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
So here it goes the solution. I'm gonna try to be succinct.
First thing, and the most important thing of the answer (almost 50%) is to admit that the pyramid grown in some pattern (I hope this is the right word). We can make some list, but I'll do it while I write the solution. With that, we can assume our conjecture in a easy way.
So, let's make our small tower's formula. This is simple:
On the first floor, we have 1 tower, on the second floor we have 2 towers, on the third floor, we have 3 towers, and this goes as far as you want to. If we sum the towers of the floors, we will get something like this:
( 1 + 2 + 3 + 4 + 5 + . . . . . . . . . . + n ) . Noticed that the number of towers in determined floor is the same of the floor's number if we count it from the top to the bottom (base of the pyramid).
This can be expressed as: t = 1 ∑ n t where n is the number of floors and t is the number of towers on determined ( n º) floor.
And this summation can be expressed as: t = 2 n ( n + 1 ) = 2 n 2 + a . This is our first formula. In order to remember which formula we will find the derived, call this A .
The second one is about the number of cards that is necessary to build the pyramid. There's something very important to be noticed:
Each floor has shapes of t small triangles pointing upwards, but the base don't have this kind of triangles. Instead, the base has n towers where each "semi-triangles" is missing one side. Look at this image:
And the last information that we need is that every triangle has 3 sides, or in this case, 3 cards.
So, agree with me: If we find the number of small towers, multiply by 3 (number of cards), and sum the difference of the cards that is missing on the base (negative value), we will have our "number of cards formula".
Let "c" be the number of cards:
c = 3 × 2 n 2 + n − n ⇒ c = 2 3 n 2 + n . Call this B
This is our second formula.
Now comes the third part, the shapes of small triangles. I'm considering the way I drew in the paint so this can be more interesting.
Now I think that the logic of these conjectures is getting more easy. Let's divided this part in two: The triangles that is pointing upwards, and other triangles that is pointing down.
Use this image in the case of some doubt shows up:
First floor, 1 triangle, second floor, 2 triangles, third floor, 3 triangles... until the base, which has no upwards triangles. The base has n small towers, so: if we find the number of towers and sum the difference of towers that it's not a triangle, we will find the number of triangles pointing upwards. Call this " k "
k = 2 n 2 + n − n ⇒ k = 2 n 2 − n
The logic for the triangle that are pointing down is the following: they only start to shows up on the second floor (if there's one), and in the base they are triangles too. So, the only thing to do is to adapt our last formula to n − 1 and no need to sum some difference. You can also look to the pyramid and notice that the number of triangles pointing upwards is the same of pointing down. But let's make our algebra: Call this " l "
l = 2 ( n − 1 ) 2 + ( n − 1 ) ⇒ l = 2 n 2 − n
Now, we already know the number of triangles, just sum the formulas (which are the same), and we have: Let number of triangles ( t ).
t = n 2 − n . Call this C .
So there it is our 3 formulas!!!
Here Mohamed imagine this pyramid as a tree (upside down, obviously).Now we calculate the derivative (which I'm gonna jump the step of explaining it because I already write a lot).
d n d A = 2 2 n + 1
d n d B = 2 6 n + 1
d n d C = 2 n − 1
Put in the place of n the value 6 8 and make the sum. The result is 4 0 8 .
I hope I made it clear.