Connect the curve
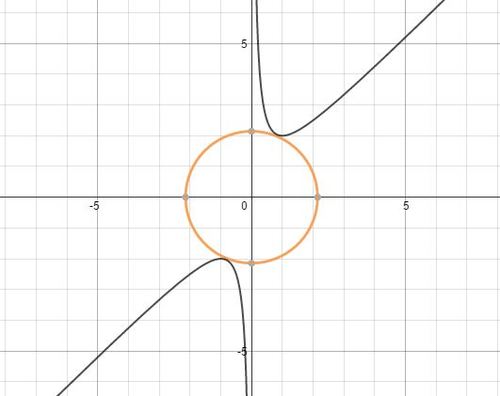 The figure shows the graph of
f
(
x
)
=
x
+
x
1
The figure shows the graph of
f
(
x
)
=
x
+
x
1
The circle is tangent to the graph in 1st and 3rd quadrant and is the smallest of its kind.
The area of the circle is in the form A π ( B + C ) where A , B , C are integers with C square free.
Find A + B + C .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
holly shitt...
I got
R
2
=
2
(
s
q
r
t
(
2
)
+
1
)
But while calculating area I mistakenly use
R
2
=
R
......
Log in to reply
Actually, you could construct bigger circles that are tangent to both components of the graph. They wouldn't be centered at the origin though.
Log in to reply
ohh I'am sorry .... I was assumed that circle must be have Cetnre (0,0) ...
I'am sorry ...... u are correct
You can also write the equation of parallel tangents on the hyperbola. Then, it is easy to see that the line joining the point of tangency of each tangent is actually perpendicular to the tangents. Which means that the normal at the points where the circle is touching the hyperbola are same as the line joining said points . From this, we can easily get the value of the two points for which such a thing occurs(using symmetry and other things).
The simplest way to do it is by using properties of discriminant. Because the circle x 2 + y 2 = r 2 only touches the curves and not crosses it, the discriminant for the equation x 2 + ( x + x 1 ) 2 = r 2 must equal to 0 .
Expanding and simplifying the equation, we get x 4 + x 2 ( 2 − r 2 ) + 1 = 0 , with b 2 − 4 a c = 0 ⇒ ( 2 − r 2 ) 2 − 4 ( 2 ) = 0 ⇒ r 2 = 8 + 2 . So the area of the circle is simply π r 2 = 2 π ( 1 + 2 ) . With A = 2 , B = 1 , C = 2 .
Yes exactly!

Because of the symmetry of f ( x ) around the origin, the centre of the circle must lie at ( 0 , 0 ) . Hence the radius is equal to the distance from the origin to ( x , y ) = ( x , x + 1 / x ) , i.e. x 2 + ( x + 1 / x ) 2 , which is what we have to minimise. Equivalently, we can find the minimum of the expression without the square root, that is:
x 2 + ( x + x 1 ) 2 = 2 x 2 + 2 + x 2 1 .
We set its derivative to zero:
4 x − x 3 2 = 0
x 4 = 2 1
x = ± 4 2 1 .
This gives a radius of:
2 x 2 + 2 + x 2 1 = 2 2 + 2 + 2 = 2 ( 1 + 2 )
therefore the area of the circle is equal to:
π ( 2 ( 1 + 2 ) ) = 2 π ( 1 + 2 )
so we obtain A = 2 , B = 1 , C = 2 and hence A + B + C = 5 .