Connect the Dots
Probability
Level
3
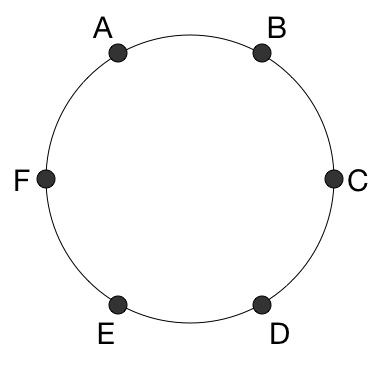
How many ways can we use 3 line segments to connect up the 6 dots, so that the line segments do not touch each other?
- Because the dots are labelled, rotations and reflections are considered distinct.
- One possible way is to connect A-B, C-D, E-F.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are 2 different types of solutions. The first is where you connect adjacent pairs of dots, for example, A-B, C-D, E-F. The other type is where you connect an opposite pair of dots, and then connect the two remaining pairs of adjacent dots, for example, A-D, B-C, E-F. The only other way we could connect the first pair of dots is by connecting one dot with the one two spots over, which would cut off the dot in the middle from being connected.
Since the orientation matters, we can work out the number of unique rotations. Solution 1 has 2 different rotations, and Solution 2 has 3 different rotations. That makes 5 solutions in all.