Connect the dots!

I evaluated the sum $\sum_{k=1}^{n-1} k(n-k)^2$ which evaluates to $\frac{1}{6} \dbinom{n^2}{2},$ begging me to believe that there is a nice bijective solution as well.

There are $n-x)(m-x)$ ways to pick an orthogonal side with side $x$ in the grid.

Apart from the square itself, there are $x - 1$ tilted squares that fit snugly inside. (Consider the possible locations for a vertex of the tilted square on the left side of the orthogonal square.)

Thus the number of possibilities, assuming that $n \leq m$ , is $S_{nm} = \sum_{x=1}^n (n-x)(m-x)x.$ In this case, $n = m = 5$ and it is easy to evaluate the sum: $S_4 = 4^2\cdot 1 + 3^2\cdot 2 + 2^2\cdot 3 + 1^2\cdot 4 = 16 + 18 + 12 + 4 = 50.$

More generally, if $n = m$ the sum can be written as $S_n = \tfrac1{12} (n-1)n^2(n+1) = \frac16\left(\begin{array}{c} n^2 \\ 2 \end{array}\right).$

Brute force but nice. I'm indebted to people on codegolf. The square is invariant under 90-degree rotations about its centre, and multiplication of a point in the complex plane by i amounts to a 90-degree rotation in that plane about the origin. Packaging those facts yields a nice solution.

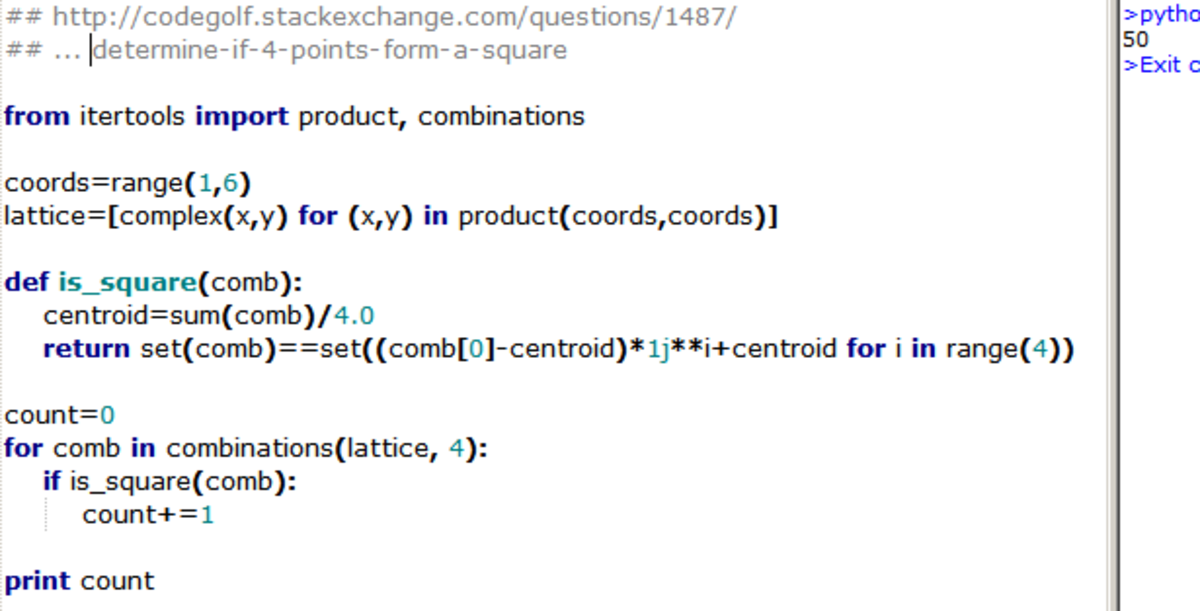
Here's a good explanation of the general solution .