Connecting Springs
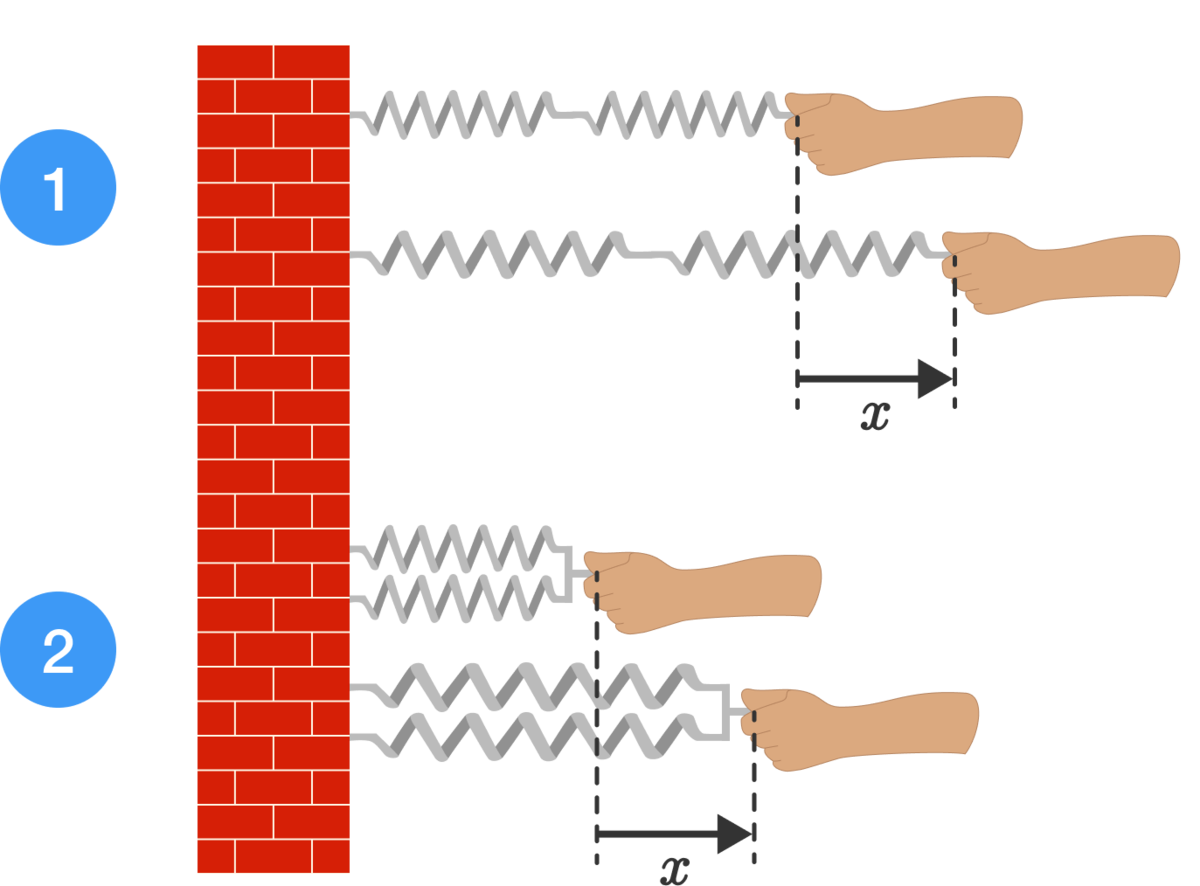
Two identical springs are arranged in the two ways shown. In the first arrangement, an amount of work is required to displace the end by a distance from equilibrium. In the second, the required work is .
What is ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let’s denote by W the amount of work required to stretch a single spring by x . Then in the second case, where the two springs are connected in parallel, each of them is displaced by x . So the amount of work is W 2 = 2 W .
In the first case, where the springs are connected in series, each one of them needs only be stretched by 2 x , which requires only a quarter of the work W . (This is because the potential energy of a single spring is quadratic in its displacement: E ( x ) = 2 1 k x 2 , where k is the spring's stiffness.) As we have two springs, we get W 1 = 2 4 W = 2 W . Therefore W 2 W 1 = 4 1 .