Consecutive side length

Geometry Level 5

$\triangle ABC$ is such that $3 \angle ABC+2 \angle BCA=180^\circ$ , and three sides of this triangle are three consecutive integers. Find the lengths of these three sides.

Let the lengths be $AB = a$ , $BC = b$ , and $CA = c$ . Write the answer as $a^{b}+c!$

Notation: $!$ denotes the factorial notation.

The answer is 83.

3 solutions

Edwin Gray
Mar 30, 2019

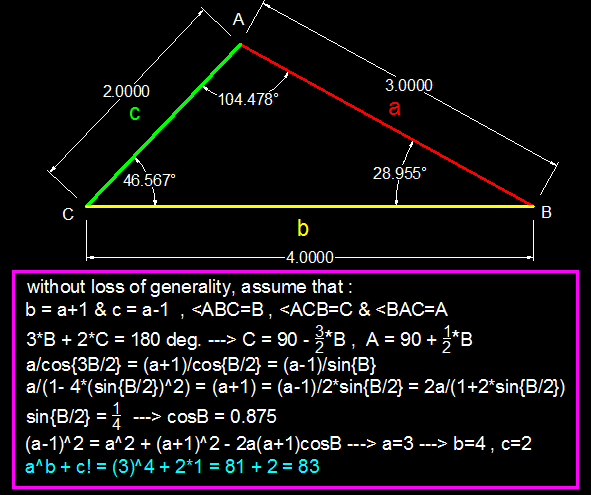
From 3B + 2C = 180, and A + B + C = 180, we get that B < C < A. Now let c = x - 1, a = x, and b = x + 1. From the Law of Cosines: (1) c^2 = a^2 + b^2 -2ab*cos(B),or substituting, (x - 1)^2 = x^2 + (x + 1)^2 - 2x(x + 1)cos(b), and B = Arccos[(x + 4)/(2(x + 1))]. Similarly, C = Arccos[(x^2 + 2)/(2(x^2 - 1))]. We then have the non-linear equation: 3B + 2C = pi to be solved numerically for x upon substituting the expressions for B and C. Newton-Raphson would work well and the solution is x = 3. So c = 2, a = 3, and b = 4. a^b + c! = 3^4 + 2! = 81 + 2 = 83.

Marta Reece
Jun 30, 2017

$3 \times \angle ABC+2 \times \angle BCA=180^0$ for this to be true, both angles have to be rather small. Smaller in fact than the two smaller angles of a triangle with sides 3, 4, and 5. The only way for three consecutive integers to have larger relative differences than those three and still form a triangle is for them to be 2, 3, and 4. It is easy to verify that this is indeed the case.

Ahmad Saad
May 1, 2016

Consecutive side length

The answer is 83.

3 solutions

0 pending reports