Consecutive Sides & Height
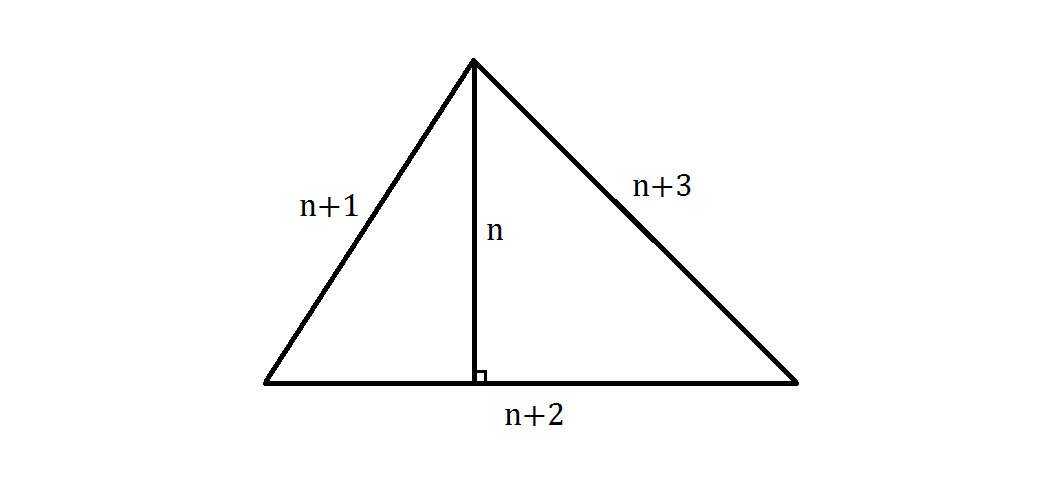 A triangle has consecutive side and height lengths for some integer
n
, as shown above.
A triangle has consecutive side and height lengths for some integer
n
, as shown above.
What is its perimeter?
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Using Pythagorean theorem, we have:
( n + 1 ) 2 − n 2 + ( n + 3 ) 2 − n 2 2 n + 1 + 6 n + 9 2 n + 1 + 2 ( 2 n + 1 ) ( 6 n + 9 ) + 6 n + 9 n 2 − 4 n − 6 n 4 − 8 n 3 + 4 n 2 + 4 8 n + 3 6 n 4 − 8 n 3 − 4 4 n 2 − 4 8 n ( n + 2 ) 2 ( n − 1 2 ) ⟹ n = n + 2 = n + 2 = n 2 + 4 n + 4 = 2 ( 2 n + 1 ) ( 6 n + 9 ) = 4 8 n 2 + 9 6 n + 3 6 = 0 = 0 = 1 2 Squaring both sides Rearranging Squaring both sides Since n = 0 is not a solution Since n = − 2 is not a solution
Therefore the perimeter is n + 1 + n + 2 + n + 3 = 3 ( 1 2 ) + 6 = 4 2 .
divide the base into two parts: the left side = x; the right side = n + 2 - x. Then we apply the Pythagorean Theorem to each side, resulting in (1) n^2 + x^2 = (n + 1)^2. (2) n^2 + (n + 2 - x)^2 = ( n + 3)^2 Expanding these equations and substituting x^2 = 2n + 1, we straightforwardly get (3) n - 2 = 2x. Expanding, n^2 - 4n + 4 = 4x^2 =8n + 4. Then n^2 - 12n = 0, or n = 12. The perimeter is then = 13 + 14 + 15 = 42. Ed Gray
Equating Heron's Formula with the standard 2 1 b h formula for the area of the triangle we get: 4 1 ( a + b + c ) ( a + b − c ) ( a − b + c ) ( − a + b + c ) = 2 1 × Base × Perpendicular height 4 1 ( 3 n + 6 ) ( n ) ( n + 4 ) ( n + 2 ) = 2 1 × ( n + 2 ) × ( n ) ( 3 n + 6 ) ( n ) ( n + 4 ) ( n + 2 ) = 2 × ( n + 2 ) × ( n ) ( 3 n + 6 ) ( n ) ( n + 4 ) ( n + 2 ) = 4 × ( n + 2 ) × ( n ) × ( n + 2 ) × ( n ) 3 ( n + 2 ) ( n + 4 ) = 4 × ( n + 2 ) × ( n ) 3 ( n + 4 ) = 4 n n = 1 2 (Notice that we can definitely cancel terms as above, since all of the factors are positive so not zero)
Therefore, Perimeter = 3 n + 6 = 4 2