Conservation of energy
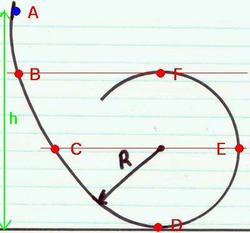 A ball of mass
m
=
5
kg is rolled, from rest, down a metal track, starting from point A as shown. Point A is
1
0
meters above the ground, and the radius of the loop in the track is
R
=
1
meters. How fast is it moving at the point D?
A ball of mass
m
=
5
kg is rolled, from rest, down a metal track, starting from point A as shown. Point A is
1
0
meters above the ground, and the radius of the loop in the track is
R
=
1
meters. How fast is it moving at the point D?
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Note, to display Latex inline, you can use normal brackets i.e. \ ( \ ) (with spaces removed). Using square brackets will make your equations take up a new line, which could be disruptive to the flow. I've edited your problem, and it is looks better. You can edit it to see what I did.
Surely the re-arrangement is v = 2 g h . Anyway, the problem specifies that the ball is rolling, so assuming that it is a uniform sphere and there is no slipping, the kinetic energy at D actually equals 1 0 7 m v 2 .
Log in to reply
yes, I also think so. If the ball is rolling, it has rotation kinetic energy. So the equation will be m g h = 2 1 m v 2 + 2 1 I ω 2
then, v = 7 1 0 g h
i am agree to every one who solved it by considering rolling because it is mentioned in problem.......plz change the answer to improve th quality of problem..
I took g=10ms^-2 and calculated the answer 20 but it said it was wrong, so I checked this solution. Please do mention the value of g otherwise confusions can happen
What will be the velocity at E and F?
At point A , potential energy=mgh=5×9.8×10=490N At point D, Potential Energy=Kinetic Energy, 490=1/ 2×M×V^2 V^2=980/5=196 V=14 m/s
It has kinetic energy 1/2 m vD2, but zero potential energy since it is at ground level (h=0 meters). So its total energy at D, ED is
E D = 1 / 2 m v D 2
Equation 8
But since energy is conserved, Ei=ED, or
m g h A = 1 / 2 m v D 2
Note that the m's cancel, and we can solve for v to get
v D = 2 g h A or the speed at point D is vD=14 m/s