Conserve Energy? - 2
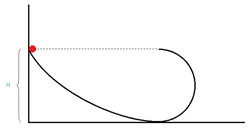 A small body starts sliding from the height
down a fixed inclined groove passing into a half circle of radius
. Find the maximum height (in m) reached by the body from ground after entering into the half circle.
A small body starts sliding from the height
down a fixed inclined groove passing into a half circle of radius
. Find the maximum height (in m) reached by the body from ground after entering into the half circle.
Given Data : &
Try more from my set Classical Mechanics Problems .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let H = 2 R .
So, velocity of particle at the lowest point of the semicircle will be V o = 4 g R . As we all know that this velocity is insufficient for the particle to go to the topmost point of the semicircle (The particle requires V o = 5 g R to go to top). Hence it will leave the semicircle at some point and start projectile motion. Let this point make an angle θ with vertical and velocity of particle at this point be V .
Since at this point particle just leave the semicircle so normal reaction given by the semicircle on the particle would be zero
⟹ m g c o s θ = R m V 2
⟹ g R c o s θ = V 2 …………………….. (i)
By conservation of energy,
2 1 m V o 2 = m g R ( 1 + c o s θ ) + 2 1 m V 2
⟹ 4 g R = 2 g R ( 1 + c o s θ ) + V 2
⟹ 2 g R = 3 V 2
or V = 3 2 g R
and c o s θ = 3 2
And velocity of particle at highest point of its trajectory would be V m a x = V c o s θ = 3 2 3 2 g R = 3 2 3 g H .
Now let x be the maximum height reached by the particle.
Using Conservation of Enengy,
m g h = m g x + 2 1 m V m a x 2
⟹ x = 2 7 2 5 H
Hence x = 5 m