Consider this
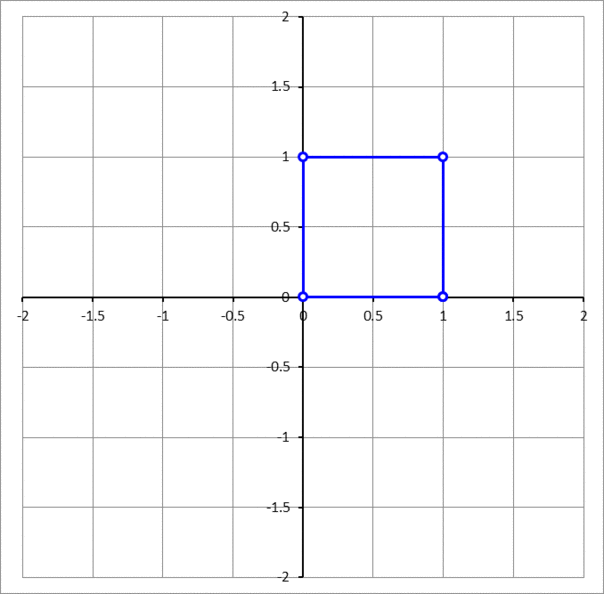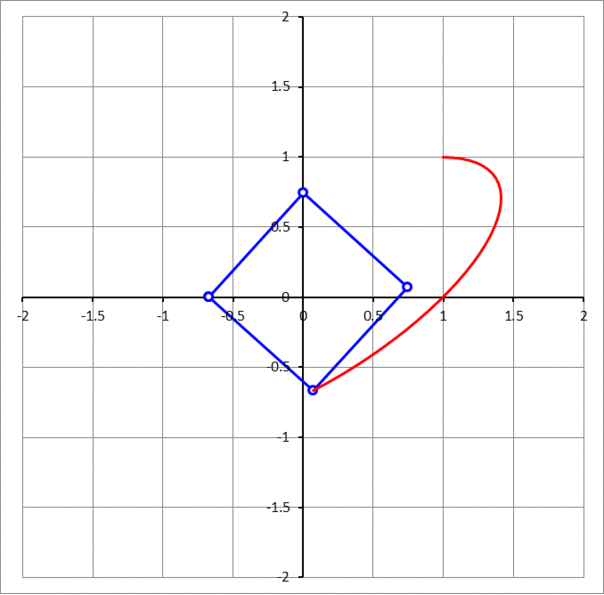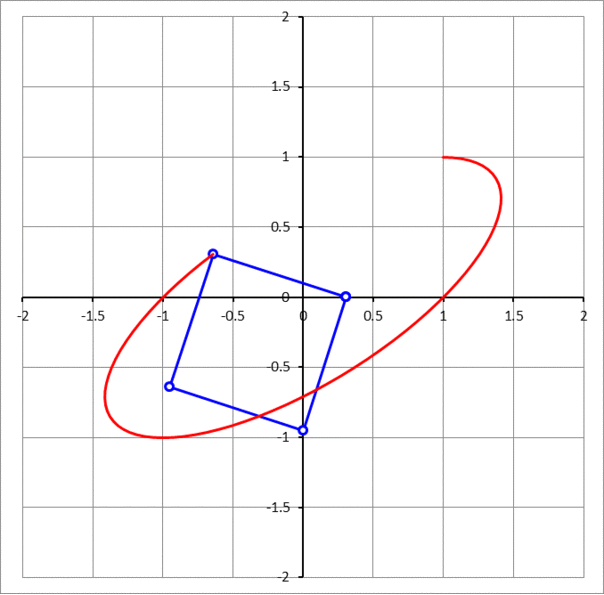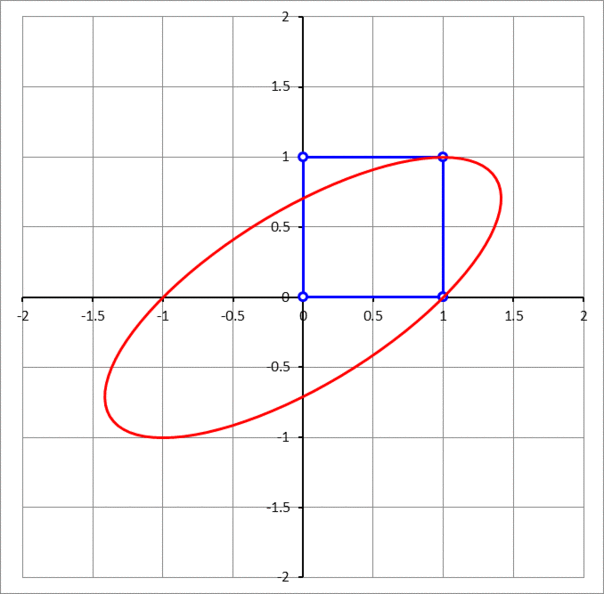
A unit square has two adjacent vertices sliding on the x - and y -axis, while the third vertex which is adjacent to the vertex sliding along the x -axis and across the square diagonal from the vertex sliding along the y -axis traces a curve. The curve is an ellipse. If θ is the angle that the major axis makes with the positive x -axis, then find tan θ . In the answer choices, ϕ is the golden ratio, ϕ = 2 1 + 5
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@David Vreken Sir, how are the triangles congruent???? I see the right angle and the unit side length, but where is the third angle???
Log in to reply
Let the angle between q and 1 in the first triangle be ∠ Q 1 and the angle between p and 1 in the first triangle be ∠ P 1 , and let the angle between q and 1 in the second triangle be ∠ Q 2 and the angle between p and 1 in the second triangle be ∠ P 2 .
From the angle sum of a triangle, ∠ Q 1 = 1 8 0 ° − 9 0 ° − ∠ P 1 = 9 0 ° − ∠ P 1 . From the straight line along the x -axis ∠ Q 2 = 1 8 0 ° − 9 0 ° − ∠ P 1 = 9 0 ° − ∠ P 1 . Therefore, ∠ Q 1 = ∠ Q 2 .
Log in to reply
Ohhh.....Wow, how did I miss this......!! Thanks Sir!!!
Let p be the x -coordinate of the vertex that slides along the x -axis and q be the y -coordinate of the vertex that slides along the y -axis.
Since the two green triangles pictured above are congruent by AAS congruence, the third vertex can be defined by x = p + q and y = p . Also, since p and q are legs of a right triangle with a unit hypotenuse, q = 1 − p 2 . Combining these equations gives x = y + 1 − y 2 which in standard form is x 2 − 2 x y + 2 y 2 − 1 = 0 .
The angle θ that the major axis makes with the positive x -axis is the same as the angle of rotation which is defined by cot 2 θ = B A − C , and since A = 1 , B = − 2 , and C = 2 , this simplifies to tan 2 θ = 2 . Using the double angle formula for tangent, tan 2 θ = 1 − tan 2 θ 2 tan θ = 2 , which solves to tan θ = 2 − 1 + 5 = ϕ − 1 .