Considering Sudoku 1
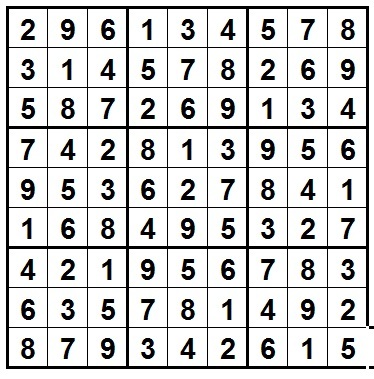
Using the rules and goals of a Sudoku puzzle, there are many thousands of possible arrangements of digits that would satisfy the conditions for a proper Sudoku solution.
Given a proper Sudoku solution, how many distinct (unique) arrangements of the digits in the grid could be presented by simply swapping the digits in individual cells?
For example, changing all the 9s to 1s and 1s to 9s would produce a different arrangement in the grid, but would still be a legitimate correct solution.
The answer is 362880.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are 9 possible digits to select from and 9 none repeating locations to place the digits
9! = 362,880 possible different arrangements.