Constrained, uneven dumbbell
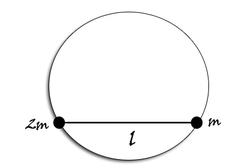 Two beads of mass
and
, connected by a rod of length
and of negligible mass, are free to move in a smooth vertical circular wire frame of radius
as shown.
Two beads of mass
and
, connected by a rod of length
and of negligible mass, are free to move in a smooth vertical circular wire frame of radius
as shown.
Calculate the velocity (in ) that should be given to the mass (when the rod is in horizontal position) in counter-clockwise direction so that the rod just becomes vertical.
Details and Assumptions:
Note: This problem appeared in our AITS (All India Test Series) - 6
The answer is 1.851.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Both masses should have same speed so that their separation remains same. So, though not specified, I assume that mass m is also given speed v
Use conservation of energy, to form the equation:
2 1 3 m v 2 = 3 m g ( 2 3 l − 6 l ) to get the answer as 1 . 8 5 1 1 .
Note If only mass 2 m is given speed v , then, there would be collision causing loss in energy. We can use conservation of angular momentum about center of loop(as both the impulses on system pass through it) to obtain the new common speed as v ′ = 3 2 v . Then the answer would have been v = 2 3 × 1 . 8 5 1 1 = 2 . 7 7