Constrained Triangle
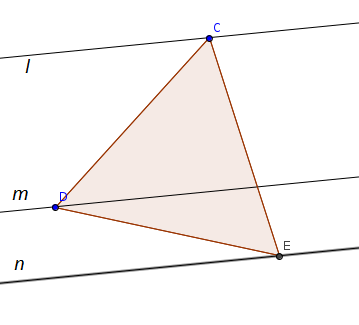
We have three parallel lines l , m and n and an equilateral triangle C D E with its vertices on these lines as shown in figure.
The distance between the lines l and m is 5 and between m and n is 2.
The side length of triangle can be expressed as A B , where A and B are positive integers with B square-free. Find A + B .
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I think there is something wrong with this question. The question said that the traingle is equilateral, which means all sides are equal in length. Also, it said the lines l,m and n are parallel. I think, based on the given information, the distances between all these lines should be the same. But in the question it confuses the reader by telling different distances between these lines. This question is confusing.
Log in to reply
the lines can have different distances, theres no reason why they cant
Not true... Since distance between pair of these lines is not same as the sides of the triangle
Log in to reply
Based on this statement "We have three parallel lines and and an equilateral triangle with its vertices on these lines as shown in fig ..." Could you Please let me know how the sides are equal and the lines are parallel and the distances are different? Please plot this with computer software and see if it is possible
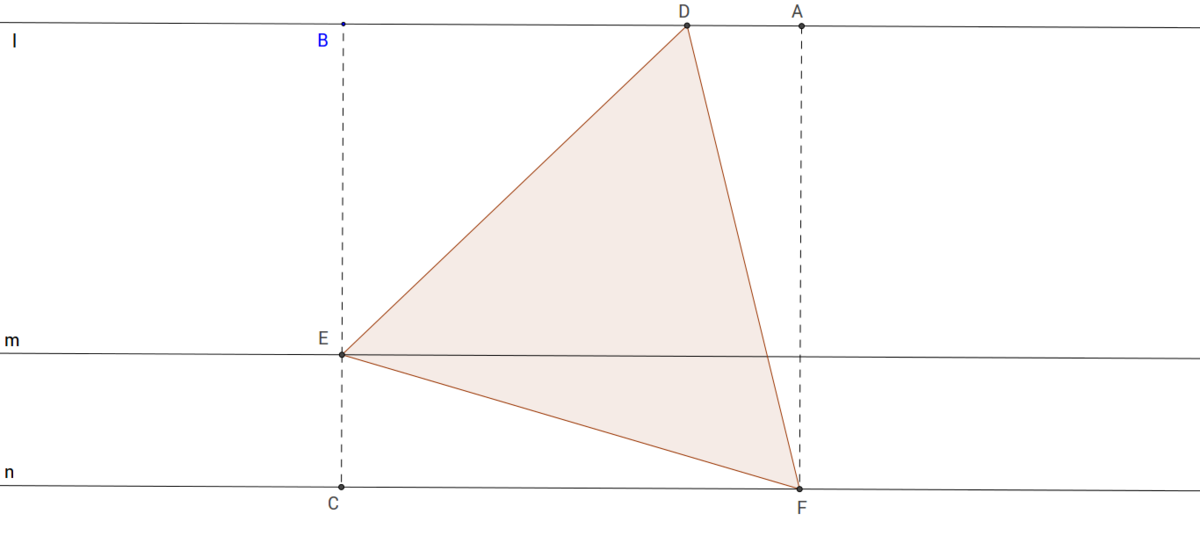
Let the side length be
a
.
Now draw altitudes
A
F
,
B
E
and
C
E
from
F
,
E
and
E
on
l
,
m
and
n
respectively.
So,
A
D
=
a
2
−
4
9
,
B
D
=
a
2
−
2
5
,
C
E
=
a
2
−
4
But
□
A
B
C
F
is a rectangle.
∴
A
D
+
B
D
=
C
F
∴
a
2
−
4
9
+
a
2
−
2
5
=
a
2
−
4
Squaring both sides and rearranging -
a
2
−
7
0
=
2
(
a
2
−
2
5
)
(
a
2
−
4
9
)
Squaring both sides and rearranging -
3
a
4
=
1
5
6
a
2
a
=
2
1
3
I did in a similiar way. But it seems a little complicated compared to the top solution.
Let CE and m intersect at Y,
EF be perpendicular to n (also m and l ) from E to meet l at F,
X the angle CEF,
and S be the sides.
So the angle DYC = 90 - X,
angle CDY=180 - (90 - X) - 60 = 30+X.
DC * SinCDY = 5, so S * Sin(30 +X) = 5.
So S * {Sin30 * CosX + Cos30 * SinX) = 5.
S * {1/2} * CosX * {1 +
3
* TanX.} = 5 ...( * )
In right triangle CEF, S * CosX= 7. ....( * * )
{ * } divide by { * * } and simplifying, TanX=
7
3
.
∴
S
=
C
F
2
+
F
E
2
=
(
7
∗
T
a
n
X
)
2
+
7
2
=
3
+
4
9
=
2
1
3
=
A
∗
B
.
∴
A
+
B
=
2
+
1
3
=
1
5
.
Consider the circumcircle of △ C D E . Let the other point of intersection between the circle and line m be called P . ∠ C P D = ∠ C E D = 6 0 ∘ , so C P = sin 6 0 ∘ 5 = 3 1 0 . Similarly, ∠ D P E = ∠ D C E = 6 0 ∘ , so C P = sin 6 0 ∘ 2 = 3 4 . ∠ C P E = 1 2 0 ∘ . By law of cosines on A D C , s 2 = C E 2 = C P 2 + E P 2 + C P ⋅ E P = 3 1 0 0 + 3 1 6 + 3 4 0 = 5 2 , so s = 2 1 3 , and our answer is 1 5 .
Let ∠ P C D = θ so that after some angle chasing we get ∠ D E Q = 6 0 − θ .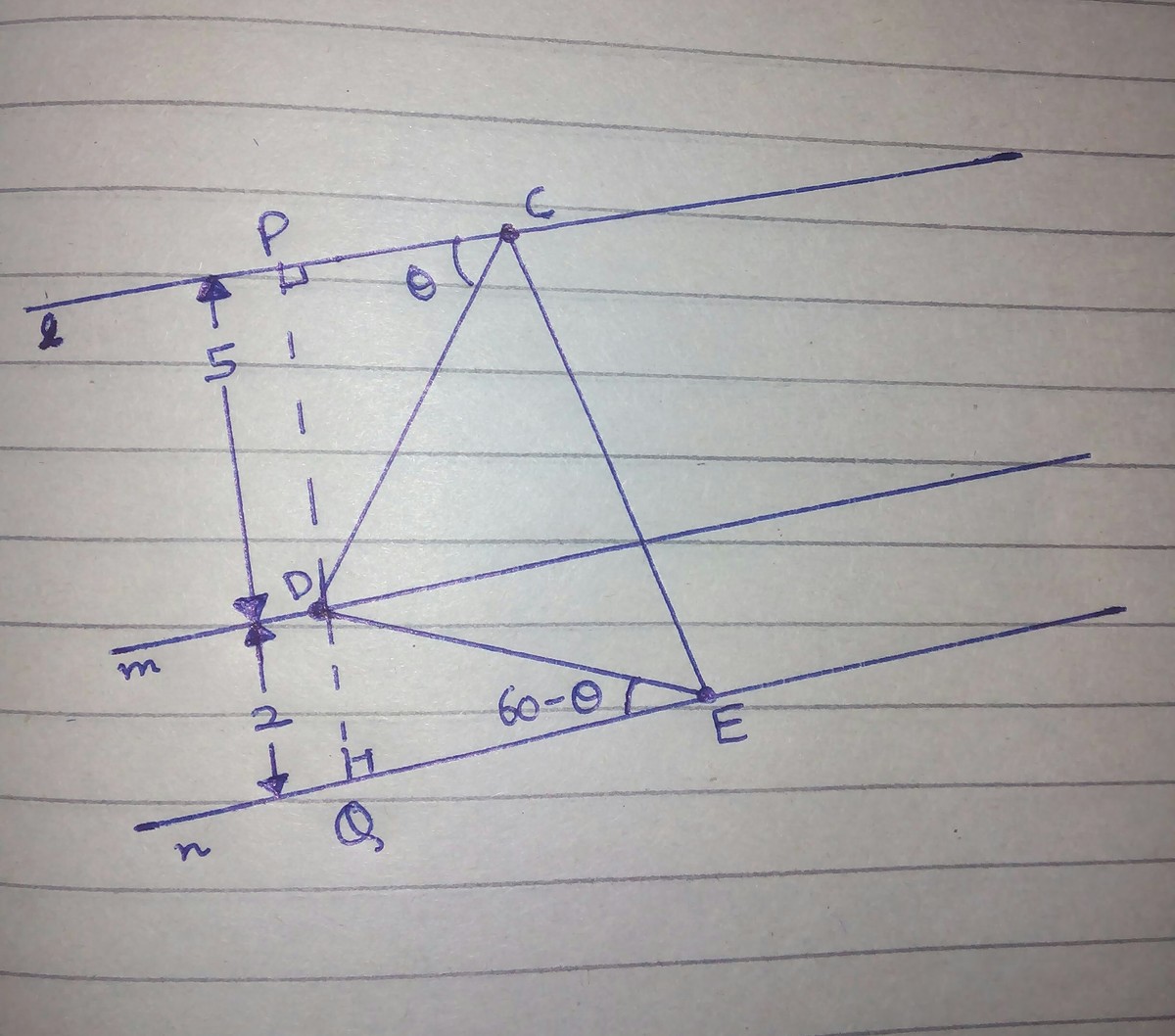
Since triangle is equilateral, ⟹ C D = D E ⟹ sin θ 5 = sin ( 6 0 − θ ) 2 ⟹ 5 ( 2 3 cos θ − 2 1 sin θ ) = 2 sin θ ⟹ 9 sin θ = 5 3 cos θ ⟹ tan θ = 9 5 3 ⟹ sin θ = 2 1 3 5
Hence, C D = sin θ 5 = 2 1 3 .
∴ 2 + 1 3 = 1 5