Construct the triangle yourself!
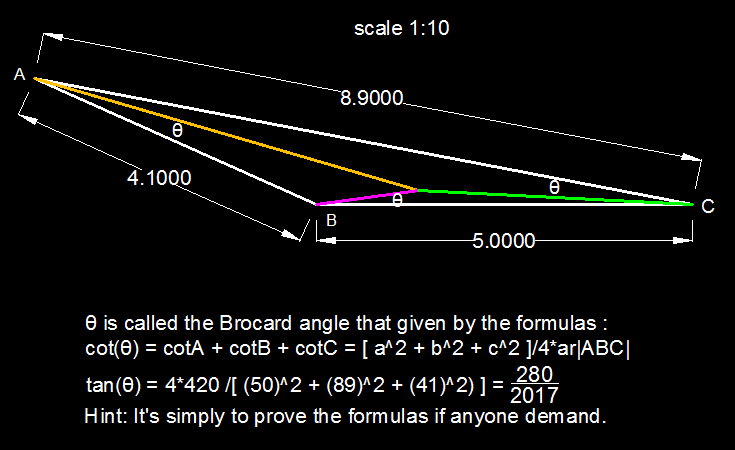
Point P is located inside △ A B C such that ∠ P A B = ∠ P B C = ∠ P C A = θ . The sides of the triangle are A B = 4 1 , B C = 5 0 and C A = 8 9 . If tan θ is of the form 2 0 1 7 k , find k .
The answer is 280.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
In general, in any Δ A B C , the angle θ as per given condition, is given by general formula
tan θ = 1 + cos A cos B cos C sin A sin B sin C
As per given question, a = 5 0 , b = 8 9 , c = 4 1
cos A = 2 b c b 2 + c 2 − a 2 = 3 6 4 9 3 5 5 1 , sin A = 1 − cos 2 A = 3 6 4 9 8 4 0
cos B = − 2 0 5 1 8 7 , sin B = 1 − cos 2 B = 2 0 5 8 4
cos C = 4 4 5 4 3 7 , sin C = 1 − cos 2 C = 4 4 5 8 4
setting all the values in above formula & simplifying, we get
tan θ = 1 + 3 6 4 9 3 5 5 1 ⋅ ( − 2 0 5 1 8 7 ) ⋅ 4 4 5 4 3 7 3 6 4 9 8 4 0 ⋅ 2 0 5 8 4 ⋅ 4 4 5 8 4
tan θ = 2 0 1 7 2 8 0
t a n θ = z P D ⟹ P D = z t a n θ
t a n θ = y F P ⟹ F P = y t a n θ
t a n θ = x E P ⟹ E P = x t a n θ
The area of triangle A B C can be solve in two ways
( 1 . )
A A B C = A A P B + A A P C + A B P C = 2 1 ( 4 1 ) ( z t a n θ ) + 2 1 ( 8 9 ) ( y t a n θ ) + 2 1 ( 5 0 ) ( x t a n θ ) = 2 1 t a n θ ( 4 1 z + 8 9 y + 5 0 x )
( 2 . ) By Heron's Formula
s = 2 4 1 + 5 0 + 8 9 = 9 0
A A B C = 9 0 ( 9 0 − 4 1 ) ( 9 0 − 5 0 ) ( 9 0 − 8 9 ) = 4 2 0
By Pythagorean Theorem, we have
x 2 + x 2 t a n 2 θ = z 2 t a n 2 θ + ( 4 1 − z ) 2 ( 1 )
y 2 + y 2 t a n 2 θ = x 2 t a n 2 θ + ( 5 0 − x ) 2 ( 2 )
z 2 + z 2 t a n 2 θ = y 2 t a n 2 θ + ( 8 9 − y ) 2 ( 3 )
Adding the three equations, we get
4 1 z + 5 0 x + 8 9 y = 6 0 5 1 ( 4 )
Going back to the area of triangle A B C , substitute ( 4 ) and A A B C = 4 2 0
A A B C = 2 1 t a n θ ( 4 1 z + 8 9 y + 5 0 x ) ⟹ 4 2 0 = 2 1 t a n θ ( 6 0 5 1 ) ⟹ t a n θ = 2 0 1 7 2 8 0
∴ k = 2 8 0