Constructible Trapezium

One easy way is to take four vertices of a regular pentagon.

https://rechneronline.de/pi/img/w/pentagon-diagonals.png

If the blue edges are the same length, then the trapezoid (if it exists) would be an isosceles trapezoid, and the diagonals would necessarily be congruent, so we can ignore one of the diagonals and examine if two isosceles triangles can make an isosceles trapezoid, as pictured below.

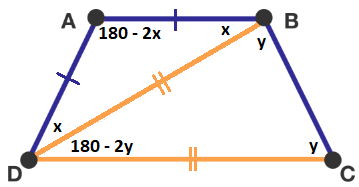
Since an isosceles triangle has congruent base angles, the base angles of $\triangle ABD$ can be labeled as $x$ and $x$ , and since the angle sum of a triangle is $180°$ , its third angle can be labeled as $180° - 2x$ (as shown above). The same reasoning can be applied to label the base angles of $\triangle DBC$ as $y$ and $y$ and its third angle as $180° - 2y$ (also shown above).

For $ABCD$ to be a trapezoid, exactly one pair of sides is parallel. In this case, $AB$ is parallel to $CD$ but $AD$ is not parallel to $BC$ , so $m \angle DAB + m \angle ADC = 180°$ which means $x + 2y = 180°$ , $m \angle CBA + m \angle BCD = 180°$ which also means $x + 2y = 180°$ , $m \angle DAB + m \angle CBA \neq 180°$ which means $x \neq y$ , and $m \angle ADC + m \angle BCD \neq 180°$ which also means $x \neq y$ .

For $ABCD$ to be an isosceles trapezoid, the upper base angles are congruent to each other and the lower base angles are congruent to each other. In this case, $m \angle DAB = m \angle CBA$ which means $3x + y = 180°$ , and $m \angle ADC = m \angle BCD$ which means $3y - x = 180°$ .

The solution $(x, y) = (36, 72)$ fulfills the four conditions ( $3x + y = 180°$ , $3y - x = 180°$ , $x + 2y = 180°$ , and $x \neq y$ ) for constructing the isosceles trapezoid with the given properties, so such a trapezoid is possible.

Start with a square, and the diagonals are longer than the bottom. Bend the edges out all the way into a straight line and the diagonals are shorter (2 lengths vs 3.) Somewhere in the middle they must be the same.

Analytic solution :

Let the coordinates of the four vertices be $A\:(-x,y)$ ; $B\:(x,y)$ ; $C\:(z,0)$ ; $D\:(-z,0)$ .

Then $AB = 2x;\ \ BC = AD = \sqrt{y^2 + (z-x)^2};\ \ CD = 2z;\ \ AC = BD = \sqrt{y^2 + (z+x)^2}.$ Equating the equations for segments of the same color and squaring, we obtain $\begin{cases} 4z^2 = y^2 + (z+x)^2 & \text{orange} \\ 4x^2 = y^2 + (z-x)^2 & \text{blue} \end{cases}$ Add the equations to see that $3(z^2 + x^2) = 2y^2;$ subtract them to obtain $4(z^2 - x^2) = 4xz.$ The latter equation can be expressed as quadratic equation in the ratio $u = x/z$ : $u^2 + u - 1 = 0\ \ \ \therefore\ \ \ u = -\tfrac12 + \tfrac12\sqrt 5 \approx 0.62\ \text{(golden ratio)},$ from which follows that $x \approx 0.62z,\ \ y \approx 1.18z.$

A lot of nice proofs on here, so I figured I'd give a heuristic:

Since DB = DC, D can be taken as the center of a circle of radius DC. Similarly, CA and CD are radii of a circle with center C and the same radius as the first circle.

So, a sufficient condition for the orange lines to all be equal is that they be radii of the two circles above.

Now, we can choose three things: the centers of the two circles and their common radius.

Once both centers are fixed, the radius must be the distance between the two. Also, wlog we can take one of the centers to be fixed. If we take the same angle (<60 degrees so blue != orange) between the radii in each circle, the lines AD and BC have equal length.

So, we have one degree of freedom left (the center of the second circle) and one constraint (AB = AD). So it seems reasonable that we can solve this problem.

Without loss of generality, assume the orange length is 1. Start with the 2 orange arms lying parallel with the orange base. At this point |AD| = |BC| = 0, and |AB| = 1.

Now, start raising the orange arms equally. |AD| & |BC| will smoothly increase, while |AB| smoothly decreases. By the time A & B are coincident (forming an orange equilateral triangle), |AD| = |BC| = 1, and |AB| = 0.

Since 1 measure increased smoothly from 0 to 1, while the other decreased smoothly from 1 to 0, at some point they were necessarily equal. That point is the required quadrilateral.

The analytical approach is beautiful. The full proof includes trigonometry and two quadratic equations.

In order for a quadrilateral to meet that property, the angle between the orange side with slope zero at the bottom and the other diagonal orange lines has to be exactly

$arccos(Φ/2)$

where $Φ$ is the golden ratio.

I’m not sure if I got this problem correct, but if I’m right: So they say that DC=DB, and we want to make sure that one of the orange vertices aren’t the same length as the blue ones, BUT if they are equal => AB=DC, AD=BC therefore it’s a square with diagonals equals to its sides, which is impossible => they are not equal and there exists quadrilateral with this configurations. If I’m not right, let me know

Fix the length of the orange edges, call this length X. Consider the length of the blue edges as we sweep the orange edges out from the position they would be in when the length of BC=AD=0. In this position, AB=X. In the final position (which is a triangle), AB=0 and BC=AD=X. Because this process is continuous, there must be a point in between when AB=BC=AD (imagine the graph, this is the point when the lines representing each length cross). This follows by the Intermediate Value Theorem. Since the orange edges are fixed, we can be sure that, at this point, the blue edges won’t be equal In length to the orange edges, since the edges along the perimeter would then form a square, and thus CD would no longer be equal to the length of the diagonals (by the Pythagorean Theorem), which is a contradiction. Therefore, this point will satisfy the conditions required.

Imagine angle ABC and angle DAB is very large, near 180 degree, in such case, AC's length will be approximately the same as AB+BC, similarly for DB, which will be approximately the same as DA+AB. In such case, DC will approximately = DA+AB+BC, so DC is longer than AC or DB

Now imagine if angle ABC and angle DAB is small so that DC almost touch each other, in such case, DC must be shorter than AC or DB.

So if there exist situations that DC can be longer or shorter than AC/DB, there must be a situation that DC can be equal to AC and DB, so the statement is possible.

I think a more simple way i just used for myself was : 1 i did not know what the qualification or meaning of the word or shape once i found out it needed 4 sides to qualify as such , i then 2 looked seen 4 sides and waalaa the answer was Yes amd was correct. Answer:Yes

Ya it is possible. U have drawn it !!

Considering extreme cases, we'll observe holding the lower base and diagonals at constant length, L. Having the two diagonals near the base puts the other base at length L, and the two legs near 0. Having the the two diagonals meet puts the other base near 0 and the two legs near L. Given this, it's clear that at some intermediate angle, the lengths of the other base and legs MUST be the same.

Jon Haussman has shown what the solution is beautifully!! But the question is merely 'is this possible' not 'find the answer'. So merely to show that it is possible! Consider drawing the orange sides first. Then ACD needs to be an isosceles triangle. (and CDB needs to be the same isosceles triangle). Note that if the angle ACD is very small then line AD is much shorter than line AB. And if angle ACD is close to 90 degrees, then now the line AD is much bigger than AB. (The angle needs to be quite a lot less than 90 degrees, and I think that in order for AB to be positive you approach (tend to) an equilateral triangle, so the limit of angle ACD seems to be 60). As angle ACD gets close to 60 the line AD is much longer than line AB. And as this angle increases from 0 the difference of between AB and AD will lessen, and become 0 at some point. | And now thanks to Jon Hausemann and perhaps others we know what the angle is that achieves equality! - 36 degrees. (So I was just showing that you would not need to know the precise answer of the angle to know that it is possible.) Regards, David

Diagonal and diameter are larger than edges.

Start with A and D together, and B and C together. Rotate CA clockwise and DB anticlockwise at the same rate.so that DA and CB remain equal. It is obvious (to me at any rate) that there must come a time when AB = DA = BC since AB starts off greater than DA or BC and will end up less than DA or BC..

In the case of a square, the diagonals are bigger than the base, and in the case of a base so big that the area of the trapezoid is almost 0, the base is greater than the diagonal, so in a moment between this two cases, u changed, and at the moment of change, the base was equal to the diagonals.

On midpoint side AD, which equal to AB even picture does not look, rise a perpendicular

Now mirror the whole picture on this new line we will get a regular petagon.

However I cannot take credit for this solution it did appear in almost an identical problem posted somewhere in BRILLIANT.