Constructing a tangent ellipse

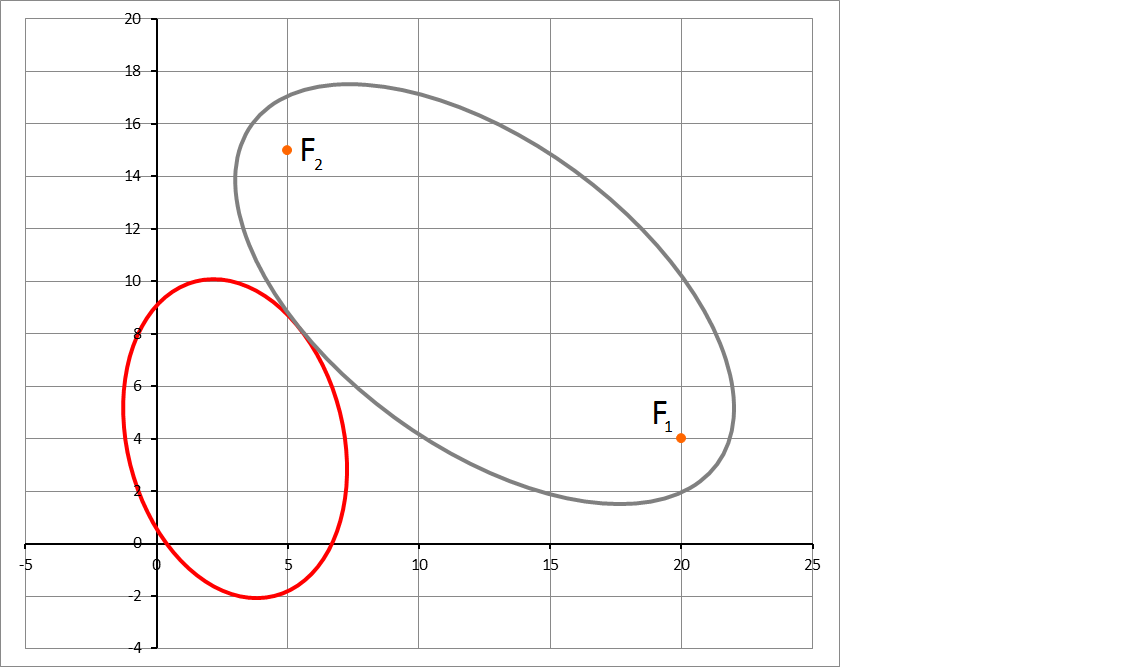
You are given an ellipse (drawn in red), which is centered at $(3, 4)$ , and has its semi-axes congruent with the vectors $(4, 1)$ and $(-1.5, 6)$ . You are also given the two points (drawn in orange), $F_1 = (20, 4)$ and $F_2 = (5, 15)$ . Now you want to construct the ellipse that has $F_1$ and $F_2$ as its focii, and is tangent to the red ellipse. Find this ellipse (drawn in gray), and submit as your answer $\lfloor 10(x_1+y_1) \rfloor + \lfloor 2 a \rfloor$ , where $(x_1, y_1)$ is the tangency point between the two ellipses, and $a$ is the length of semi-major axis of the constructed ellipse, and $\lfloor \cdot \rfloor$ is the floor function, for example, $\lfloor 3.7 \rfloor = 3$ .