Constructing four digits (Brian is bored again)

1/9999
= 0.0001000100010001...

1/9999²
= 0.00000001000200030004...

1/9999³
= 0.000000000001000300060010...

The first nominator represent 1 in all repetition, the second with n, and the third with n(n + 1)/2.

Given that 1/9999 + 7/9999² + 12/9999³ + x/9999⁴ represented the given 'cubic' series, we have :

n = 1, 0001 = 1 × 1
n = 2, 0008 = 1 × 1 + 7(n – 1) = 1 + 7
n = 3, 0027 = 1 × 1 + 7(n – 1) + 12 × [(n – 2)(n – 1) / 2] = 1 + 7 × 2 + 12

n = 4, 0064
= 1 × 1 + 7 × (n – 1) + 12 × [(n – 2)(n – 1) / 2] + x × [(n – 3)(n – 2)(n – 1) / 6]
= 1 + 7 × 3 + 12 × 3 + x(1 × 2 × 3 / 6)
= 1 + 21 + 36 + x(1)
= 58 + x
x = 64 – 58 = 6

Note that a linear sequence increases constantly, while quadratic sequence has an increase of increase that is constant, and cubic sequence has an increase of an increase of an increase that is constant.

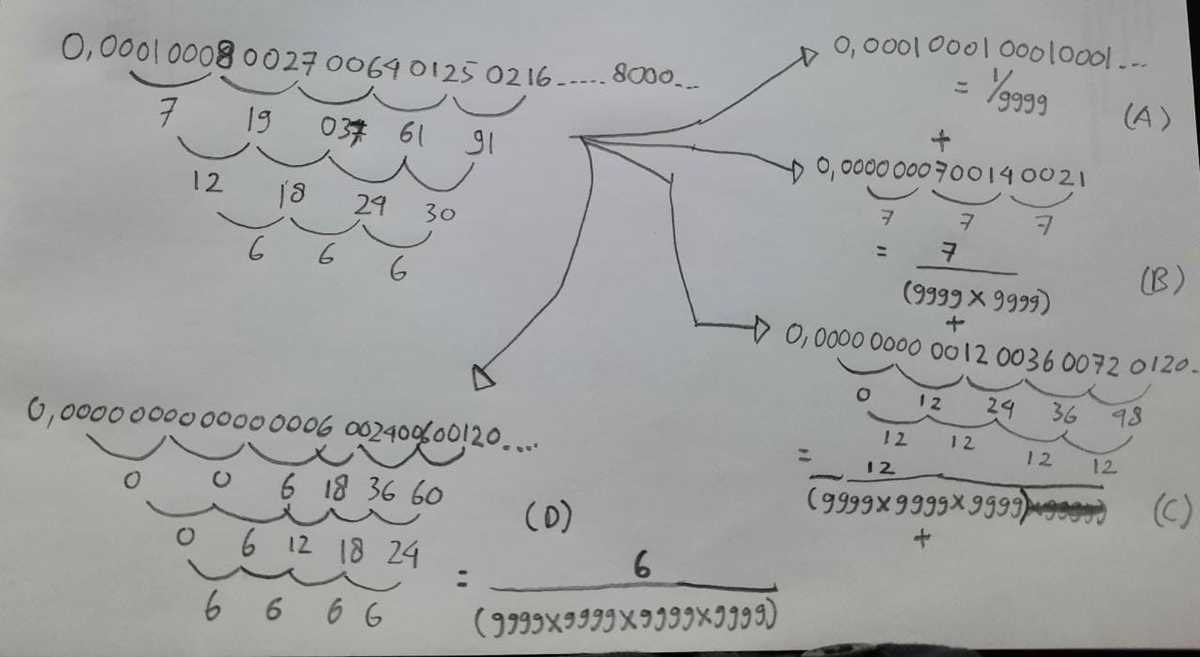
One of the possible approach to this problem is by solving it as 4 possible parts, part A being a constant recurring number, part B being a constant increasing sequence, part C as the part with constant increase of increase, while part D is a constant increase of increase of increase. You can see that each part is constructed from the first number, the first increase, the first increase of increase, and the constant increase of increase of increase.

We also have known that for any integer m, $\frac{m}{9999}$ = $(\frac{1}{10000}) \times m + (\frac{1}{10000}) \times (\frac{1}{10000}) \times m + (\frac{1}{10000}) \times (\frac{1}{10000}) \times (\frac{1}{10000}) \times m + .....$

From that, we can easily solve part D as well as other parts. In part D,

0.0006000600060006.... when divided with 9999 will becomes 0.000000060012001800240030.....

When divided further with 9999, it will look like a sequence whose increase is increasing, which is 0.000000000006001800360060...

When divided again with 9999, the digit after decimal will have a constant increase of increase of increase.

Now we only need to solve each part and sum them to get the cubic sequence we want.

And another problem for the generalized geometric series - yay! For simplicity, let $q=10^{-4}$ and Brian's latest number be $X$ . Then we rewrite $k^3$ as a sum of four binomial coefficients so that we may use the generalized geometric series: $\begin{aligned} X &= \sum_{k=0}^\infty k^3q^k = \sum_{k=0}^\infty \left[ 6\binom{k+3}{k} - 12\binom{k+2}{2} +7\binom{k+1}{1}-\binom{k+0}{0} \right]q^k\qquad \left|Q:=10^4=q^{-1}\right.\\[1em] & \underset{(*)}{=}\frac{6}{(1-q)^4} -\frac{12}{(1-q)^3} + \frac{7}{(1-q)^2} - \frac{1}{1-q} = \frac{6Q^4}{(Q-1)^4} -\frac{12Q^3}{(Q-1)^3} + \frac{7Q^2}{(Q-1)^2} - \frac{Q}{Q-1} =\frac{Q^3+4Q^2+Q}{(Q-1)^4} \end{aligned}$ To compare $X$ with the coefficients given by the teacher, we rewrite $X$ with partial fraction decomposition (PFD). The last coefficient would already be enough: $X\underset{\text{PFD}}{=} \frac{1}{Q-1} + \frac{7}{(Q-1)^2} + \frac{12}{(Q-1)^3}+\frac{\boxed{6}}{(Q-1)^4}$

---

The generalized geometric series:

$\begin{aligned} \sum_{k=0}^\infty \binom{k+n}{k}q^k&=\frac{1}{(1-q)^{n+1}},&&&|q|&<1, &n&\in\mathbb{N}&(*) \end{aligned}$