Constructing this is harder than solving it!

triangle OMC is similar to triangle OAB. and MC:AB=1:2. Therefore, OC:OA=1:2.

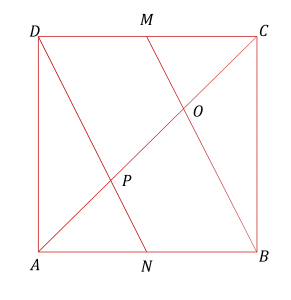Draw a line $DN$ to midpoint of $AB$ .

The lines $MB$ and $DN$ divide the diagonal into three equal segments because $CM=MD$ implies $CO=OP$ and $BN=NA$ implies $OP=PA$ .

So $\frac{OC}{OA}=\frac{1}{2}$ .

By using pythagoras theorem i find the hypotenuse AC=4√2 now, AC= $3\times OC$ . so, OC= $\frac{4√2}{3}$ and OA= $2\times OC$ . so, OA= $\frac{8√2}{3}$ According to the question OC:OA= $\frac{4√2}{3}$ : $\frac{8√2}{3}$ =1:2 so, the answer is 3. Sorry I can't draw the picture.

I did it by making lines of the form $y = mx + b$ for $\overline{AC}$ and $\overline{BM}$ , and using D, or the bottom left corner of the square, as the origin on a coordinate plane. Then I found the intersection $O$ of the two lines to be $(\frac{8}{3},\frac{4}{3})$ . Then I simply found the distance from $O$ to the x-intercept of $\overline{AC}$ , the length of line $\overline{OC}$ , which was $\frac{4\sqrt{2}}{3}$ . Then I found the distance from $O$ to the y-intercept of $\overline{AC}$ , the length of $\overline{OA}$ , which was $\frac{8\sqrt{2}}{3}$ . Dividing them I got $\frac{1}{2}$ , so the answer was $1 + 2 = \boxed{3}$ .

Solution:

1. find the equations of the line

   a. line AC is an identity with negative y so, x = -y

   using (y-y1) = (y2-y1)(x-x1)/(x2-x1)
   

   b. line BM is y = 2x - 8

2. Find the intersection

   a. y= -x ; -x = 2x - 8; so x = 8/3 and y = -8/3

3.AC=sqrt((2(4^2 )))=4√2 ; AO= sqrt((2(8/3)^2 ))=8/3 √2

1. AC - AO = OC = 4√2- 8/3 √2 = 4/3 √2

2. a = AC ; b =AO ; a/b=1/2 ; a+b=3