Construction Is A Piece Of Cake! Right? (Part-3)
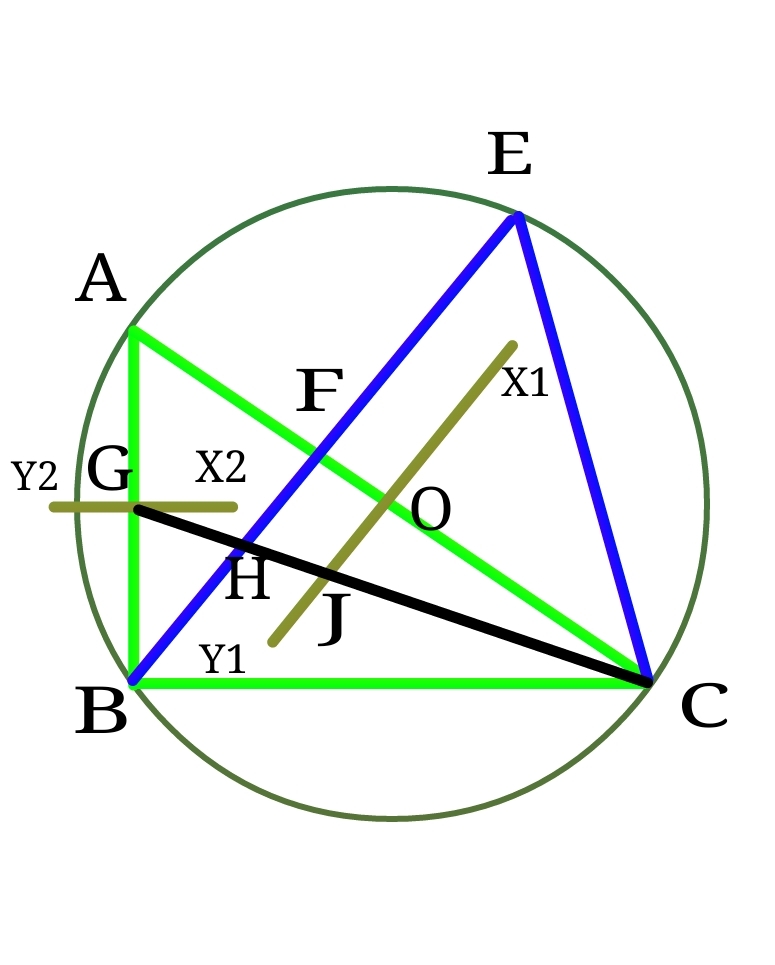
Mohit, influenced by Akshat and Anshuman , took a right (right angled at ), where and , and started doing aimless constructions, the steps of which are given below:
( ) He drew perpendicular bisector of which intersects at a point and another perpendicular bisector of which intersects at a point .
( ) Then he constructed a circle taking center and radius of the circle as . Then he constructed an which is equal to such that lies on the circle.
( ) He then joined which meets at .
( ) Then he joined which intersects at and at .
Mohit then wondered what could possibly be equal to.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
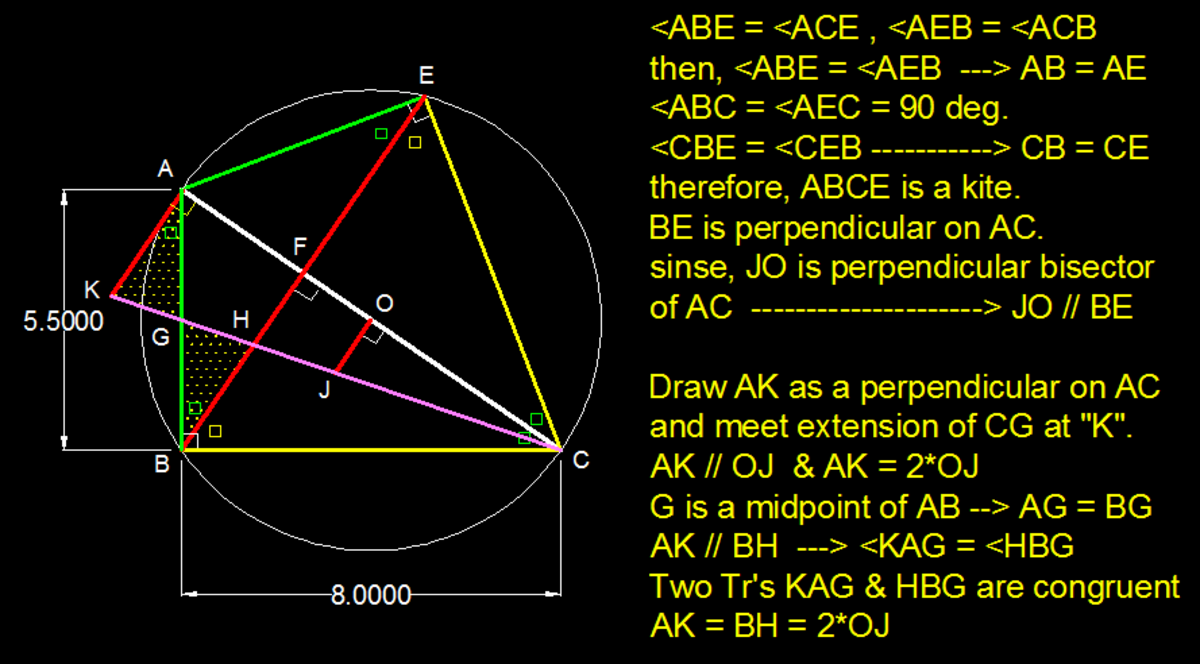
Join B O which intersects C G at I
Notice that in △ A B C , B is the orthocenter, I is the centroid and O is the circumcenter.
Hence, B O is Euler line .
So I O B I = 2 . Also, △ B I H ∼ △ J I O , so O J B H = I O B I = 2 .