Construction is must
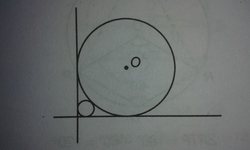A circle placed against a right angled triangle centred at O is the 14 cm radius.What is the radius of the smaller circle placed in the remaining gap?
The answer is 2.4020.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
Clear setup! The picture helps make it easy to see how you solved the problem.
Same method.
Distance from the point of tangency of the circles from the origin.-the
gap-=
(
1
4
∗
2
−
1
4
)
.
B
u
t
t
h
i
s
i
s
a
l
s
o
d
i
s
t
a
n
c
e
o
f
O
1
a
n
d
o
r
i
g
i
n
+
x
=
2
∗
x
+
x
=
1
4
(
2
−
1
)
.
∴
x
=
1
4
∗
2
+
1
2
−
1
=
2
.
4
0
2
0
Let x be the radius of smaller circle, Applying pythagoras theorem in triagle O P O ′ (see figure).
⇒ ( 1 4 + x ) 2 = ( 1 4 − x ) 2 + ( 1 4 − x ) 2 ⇒ 1 4 + x = 2 ( 1 4 − x ) x = 1 4 ( 2 + 1 2 − 1 ) = 2 . 4 0 1