Construction Is A Piece Of Cake, Right?

Geometry Level 4

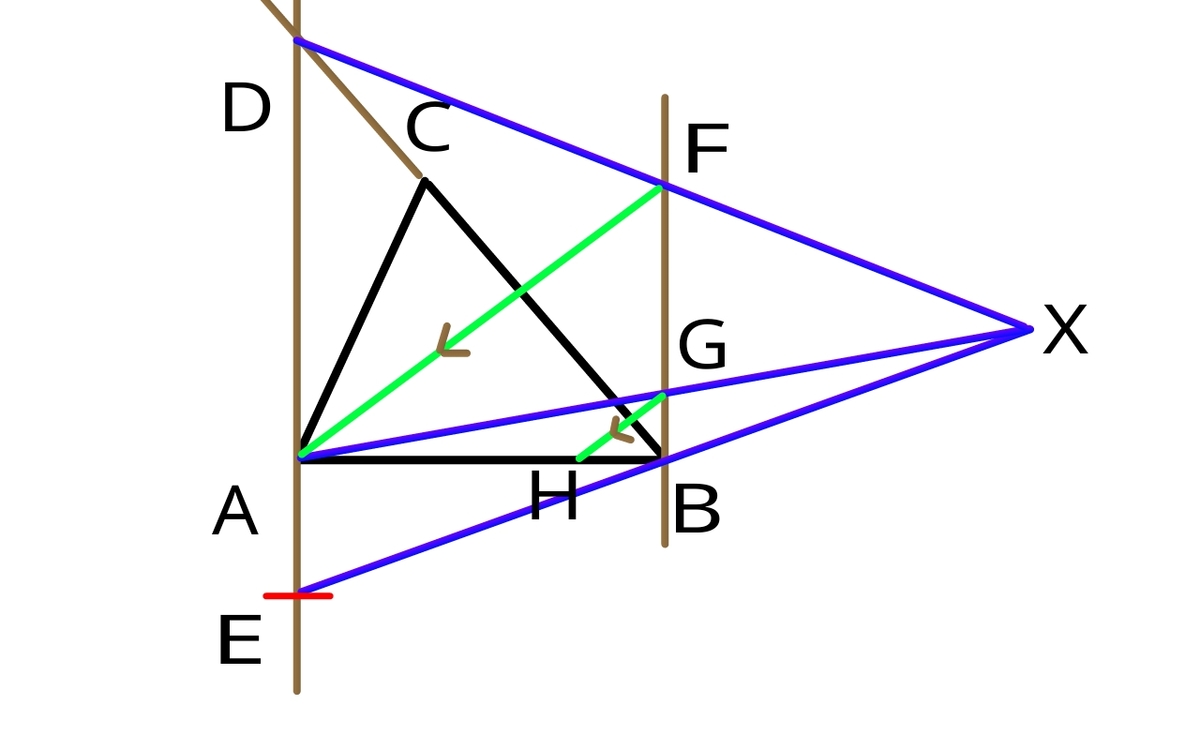
Anshuman took an arbitrary triangle $ABC$ and started doing aimless constructions, the steps of which are given below:

( $1$ ) Through points $A$ and $B$ , he drew two lines perpendicular to segment $AB$ . He extended $BC$ where it intersected with the perpendicular at $D$ and chose an arbitrary point $F$ on perpendicular drawn from $B$ .

( $2$ ) Then he cuts an arc equal to $BD$ on $AD$ taking centre $D$ , he names that point $E$ .

( $3$ ) Then he joins $DF$ and $EB$ and extend them up to the point of intersection $X$ .

( $4$ ) Then he joined $A$ with $X$ and name their intersection with $BF$ as $G$ .

( $5$ ) Then he joined $AF$ and drew a parallel to it from $G$ which intersects $AB$ at $H$ .

He wonders: "What $AH$ possibly be equal to?"

Disclaimer : Image not drawn up to scale.

Median of triangle drawn from Point

B

AC

Median of triangle drawn from Point

A

BC

Altitude of triangle drawn from Point

B

AC

Altitude of triangle drawn from Point

A

BC

Circumradius of the triangle

ABC

Inradius of the triangle

ABC

Nothing can be said

2 solutions

Akshay Yadav
Mar 18, 2016

This problem is a result of real life experience, my friend Anshuman and I were actually trying to find our own way of constructing altitude of triangle.

The problem is based on practical application of Basic Proportionality Theorem (BPT),

In the above figure it can be clearly seen that $\frac{CA}{CB}=\frac{AB}{BD}$ by similarity of triangles.

In the problem also we try to achieve the same by construction,

First we extend the sides to form a right triangle $DAB$ , in the next step we take the length of $DB$ on $DA$ (extended) and mark the point as $E$ .

Now,

$\frac{DB}{DA}=\frac{DE}{DA}$

As $FB$ is parallel to $DE$ ,

By BPT the ratio continues,

$\frac{DE}{DA}=\frac{FG}{GB}$

Again as $FA$ is parallel to $GH$ ,

$\frac{FG}{GB}=\frac{AH}{HB}$

Hence we make $\frac{DB}{DA}=\frac{AH}{HB}$ .

That makes $AH$ equal to the altitude drawn from $A$ on $BC$ .

How is $\frac{DB}{DA}=\frac{DB}{DE}$ ?

For, $\frac{DB}{DA}=\frac{DB}{DE}\Rightarrow DA=DE$ which is a contradiction.

A Former Brilliant Member - 5 years, 2 months ago

Its a mistake, thanks for stating it, I will correct it.

Akshay Yadav - 5 years, 2 months ago

Michael Mendrin
Mar 18, 2016

From inspection of the graphic, there can only be $2$ possible answers. Either $AH$ equals the altitude of the triangle $ABC$ from $A$ to $BC$ , or "nothing can be said". The reason for his is because the construction is independent of where point $C$ is along the line $DB$ , which rules out all the other answers. Then we just focus on whether or not it's really the altitude.

Construction Is A Piece Of Cake, Right?

2 solutions

0 pending reports