Construction Time
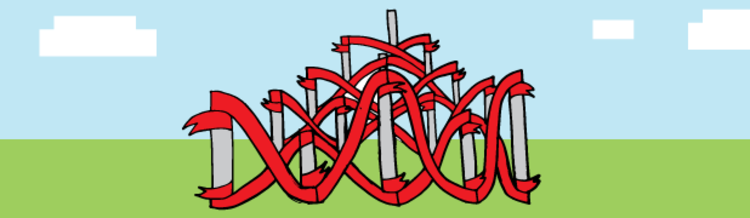 In a construction project, Joe decides to stick up
vertical poles, of lengths
,
,
,
, and
. Each pair of consecutive poles have diagonal strands attached from the top of one pole to the bottom of the other. From the intersection of these diagonal strands, more poles are vertically stuck up. Using only the new poles, this process is repeated until one pole remains. To the nearest thousandth, find the length of this pole.
In a construction project, Joe decides to stick up
vertical poles, of lengths
,
,
,
, and
. Each pair of consecutive poles have diagonal strands attached from the top of one pole to the bottom of the other. From the intersection of these diagonal strands, more poles are vertically stuck up. Using only the new poles, this process is repeated until one pole remains. To the nearest thousandth, find the length of this pole.
This problem is part of Tristan's set Formulas and Theorems .
The answer is 0.237.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you draw a diagram with line segments of lengths 1,3,5,7,9 perpendicular to the ground and draw diagonals from the top to bottom of the consecutive pole, you create a set of similar triangles. Solving for the height of the intersection above the ground reveals that the height above the ground is always (product of heights)/(sum of heights). Repeating this process with the new poles created in the previous run until you get the height of the last two poles (35/96, 315/464) you find the answer is 315/1328