Continued Factorial Fractions

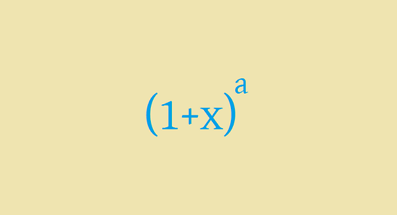By definition, $e$ is given by the Taylor Expansion given in the question. Hence, answer is $e$ , approximately $2.71$ .

Applying the binomial theorem to the limit definition of e, one gets 1/0!+1/1!+1/2!+1/3!+1/4!+…

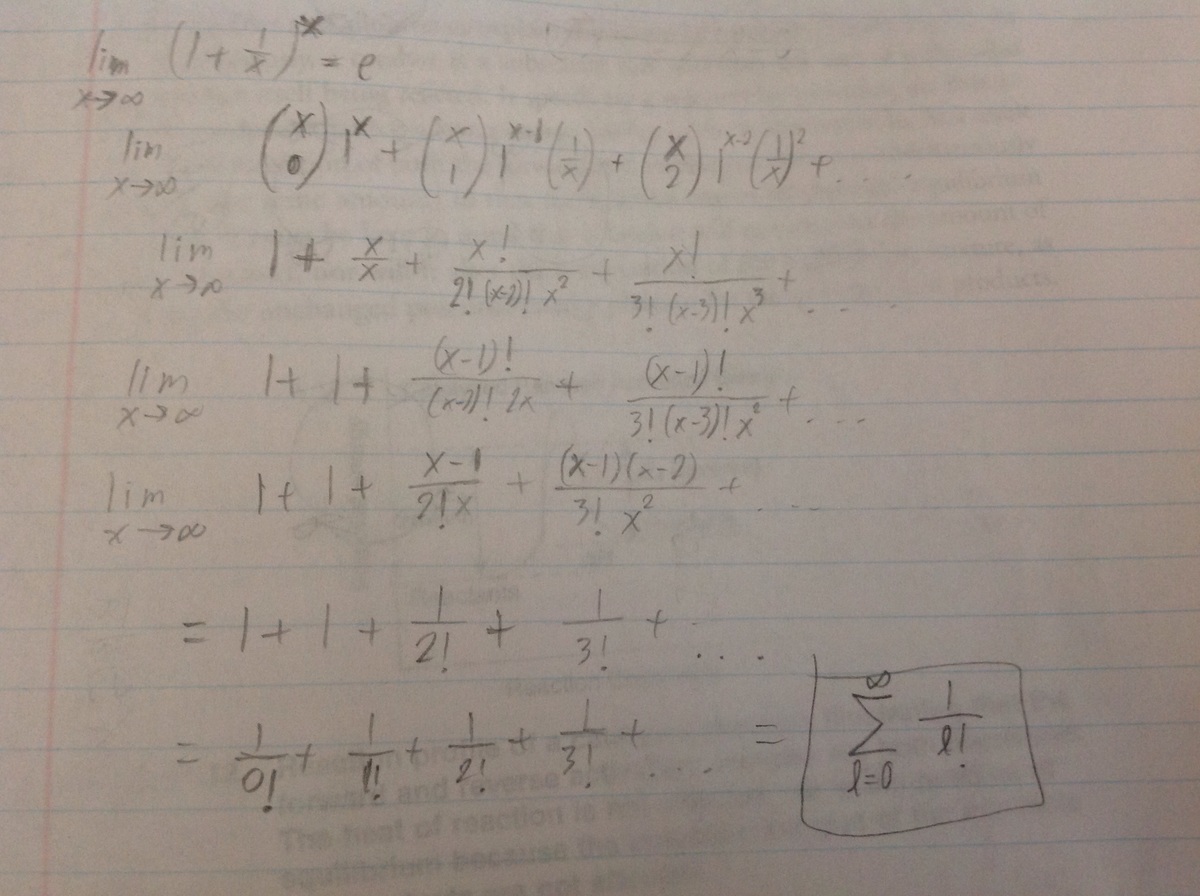
Therefore the answer is e.

The given series is the expansion of $e^x$ . Here x=1. Thus, the value of series is $e^1$ $\Rightarrow$ 2.71

Python 2.7:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

from math import factorial as fac
from fractions import Fraction as frac
from time import time
total = 0
denominator = 0
end = time() + 10
while time() < end:
    total += frac(1,fac(denominator))
    denominator += 1
print "Answer:", float(total)

The number is $e$ (Euler's Number). It is a irrational number, so you cannot define its exact value but you can get close to it.

You can either get a rough value by calculating the value of first few fractions (This works because the value of each fraction starts decreasing as you move towards right and after a few calculations, the value almost becomes negligible) -

$1+1+\frac { 1 }{ 2 } +\frac { 1 }{ 6 } +\frac { 1 }{ 24 } +\frac { 1 }{ 120 } =2.718055556$

Or you can calculate a more accurate value of it using this formula -

${ (1+\frac { 1 }{ n } ) }^{ n }$

where $n$ is a very large number. As $n$ approaches infinity, the expression above approaches $e$ .