Continuous functions satisfying a given condition

By completing the square, for all real numbers $x$ , we have

$\begin{aligned} & {{\left( f\left( x \right) \right)}^{2}}+{{x}^{4}}=x\left( 1+{{x}^{2}} \right)f\left( x \right) \\ & \Leftrightarrow {{\left( f\left( x \right) \right)}^{2}}-2\frac{x}{2}\left( 1+{{x}^{2}} \right)f\left( x \right)+{{\left[ \frac{x}{2}\left( 1+{{x}^{2}} \right) \right]}^{2}}={{\left[ \frac{x}{2}\left( 1+{{x}^{2}} \right) \right]}^{2}}-{{x}^{4}} \\ & \Leftrightarrow {{\left[ f\left( x \right)-\frac{x}{2}\left( 1+{{x}^{2}} \right) \right]}^{2}}={{\left[ \frac{x\left( {{x}^{2}}-1 \right)}{2} \right]}^{2}} \ \ \ \ \ (1) \\ \end{aligned}$ Let $g\left( x \right)=f\left( x \right)-\dfrac{x}{2}\left( 1+{{x}^{2}} \right)$ , $x\in \mathbb{R}$ . Then, $g\left( x \right)=0\overset{(1)}{\mathop{\Leftrightarrow }}\,\dfrac{x\left( {{x}^{2}}-1 \right)}{2}=0\Leftrightarrow x=0$ , or $x=\pm 1$ . Since $g$ is continuous, in the intervals defined by any two consecutive zeros, $g(x)$ maintains a positive or a negative sign and is equal either to $\dfrac{x\left( {{x}^{2}}-1 \right)}{2}$ , or $-\dfrac{x\left( {{x}^{2}}-1 \right)}{2}$ .

Consequently, in every interval, either $f\left( x \right)=g\left( x \right)+\frac{x}{2}\left( 1+{{x}^{2}} \right)=\frac{x\left( {{x}^{2}}-1 \right)}{2}+\frac{x}{2}\left( 1+{{x}^{2}} \right)={{x}^{3}},$ or $f\left( x \right)=g\left( x \right)+\frac{x}{2}\left( 1+{{x}^{2}} \right)=-\frac{x\left( {{x}^{2}}-1 \right)}{2}+\frac{x}{2}\left( 1+{{x}^{2}} \right)=x.$ For the four intervals $\left( -\infty ,\ -1 \right)$ , $\left( -1 ,\ 0 \right)$ , $\left( 0 ,\ 1 \right)$ , $\left( 1 ,\ + \infty \right)$ , there are ${{2}^{4}}=16$ different combinations. Hence, the number of different continuous functions $f$ that satisfy the given equation is $\boxed{16}$ .

Rewrite the equation. $\\ \left(f\left(x\right)\right)^2+x^4 = x\left(1+x^2\right)f\left(x\right) \\ \left(f\left(x\right)\right)^2-x\left(x^2+1\right)\left(f\left(x\right)\right)+x^4 = 0 \\$ Use the quadratic equation to isolate $f\left(x\right)$ $\\ f\left(x\right) = \frac{x\left(x^2+1\right) \pm \sqrt{\left(x\left(x^2+1\right)\right)^2-4x^4}}{2} \\$ We cannot just take two solutions as plus and with minus. The plus-minus symbol can be either positive or negative at any point. To see what to do to stay continuous, we must transform the equation further. $\\ f\left(x\right) = \frac{x\left(x^2+1\right) \pm \sqrt{x^2\left(x^2+1\right)^2-4x^4}}{2} \\ f\left(x\right) = \frac{x\left(x^2+1\right) \pm \sqrt{x^2\left(\left(x^2+1\right)^2-4x^2\right)}}{2} \\ f\left(x\right) = \frac{x\left(x^2+1\right) \pm \sqrt{x^2\left(\left(x^4+2x^2+1\right)-4x^2\right)}}{2} \\ f\left(x\right) = \frac{x\left(x^2+1\right) \pm \sqrt{x^2\left(x^4-2x^2+1\right)}}{2} \\ f\left(x\right) = \frac{x\left(x^2+1\right) \pm \sqrt{x^2\left(x^2-1\right)^2}}{2} \\ f\left(x\right) = \frac{x\left(x^2+1\right) \pm \left(x\left(x^2-1\right)\right)}{2} \\ f\left(x\right) = \frac{x\left(x^2+1\right) \pm \left(x-1\right)\left(x\right)\left(x+1\right)}{2} \\$ The plus-minus term is zero at and only at x equaling negative one, zero, or positive one. This gives us four regions: $x<-1,-1<x<0,0<x<1,1<x$ . To stay continuous, whether the plus-minus sign "acts" as a positive or negative sign must be the same within the region, as within the region the plus-minus term is never zero. The four regions, however, may have different signs from each other.

Each of these four values has a binary choice, either plus or minus. This gives us a total number of possibilities of $2^4=16\\$ Perhaps this can be seen more clearly with a graph: 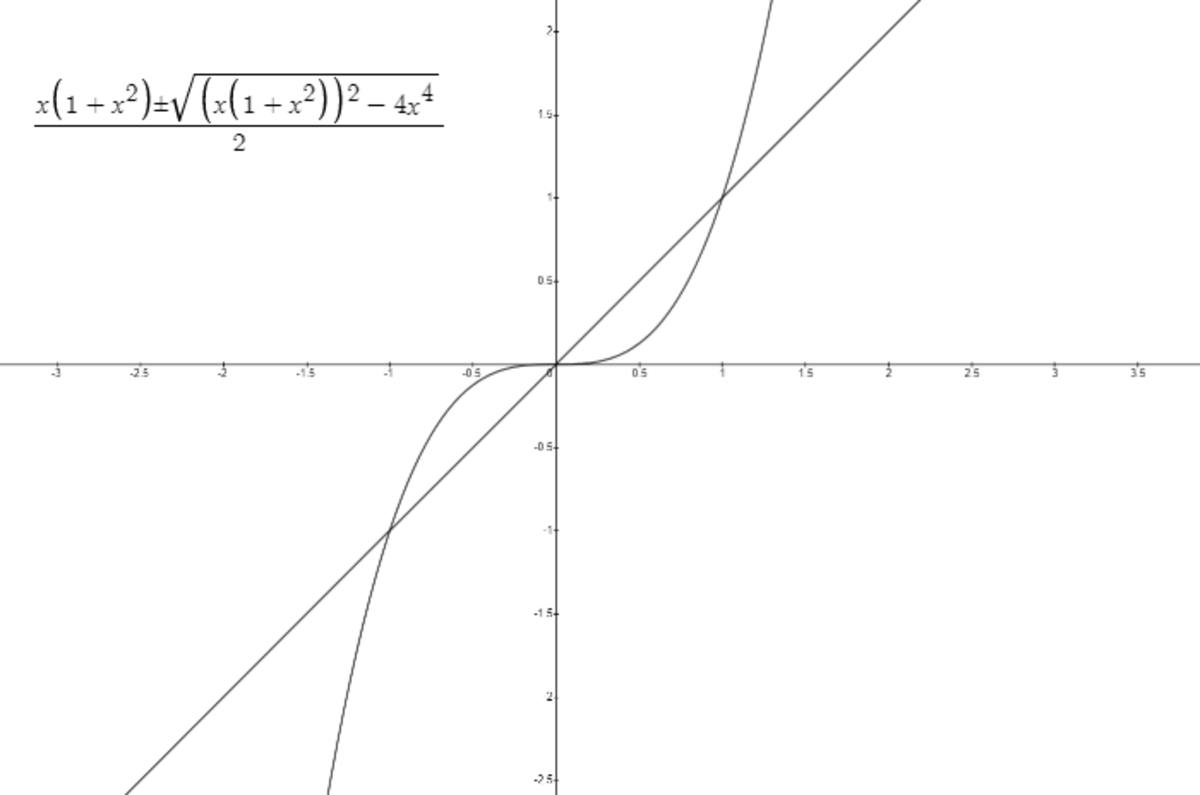We can clearly see that to keep the graph a function and continuous, there must be a choice in 4 regions of taking the "top-half" or "bottom-half" of the region. Apologies if this doesn't make much sense, this is just how it makes the most sense to me.

Let $y=f(x).$ Then the equation factors: $(y-x)(y-x^3) = 0.$ When $x = -1,0,1,$ we get $y = -1,0,1$ respectively. These are the only intersection points of $y=x$ and $y=x^3.$ So the general form is $f(x) = \begin{cases} f_1(x) & x \le -1 \\ f_2(x) & -1 \le x \le 0 \\ f_3(x) & 0 \le x \le 1 \\ f_4(x) & 1 \le x \end{cases}$ where $f_i(x) = x$ or $f_i(x) = x^3$ for all $i.$ Since there are two choices for each $i,$ there are $2^4 = 16$ choices for $f.$