Controversial Limit?

Let $y=tx$ for some positive number $t$ .

Then the given equation becomes

$\left( tx \right) ^{x} = x ^{tx}$ .

Raise both sides to the power $\frac{1}{x}$ and divide by $x$ to get

$t=x^{t-1}$ .

Now we have parametric expression for $x$ and $y$

$x=t^{\frac{1}{t-1}}$ ,

$y=t^{\frac{t}{t-1}}$ .

Since $t=\frac{y}{x}$ , $t$ approaches $1$ when $x$ approaches $y$ .

We can show both $x$ and $y$ approaches $e$ when $t$ approaches $1$ using simple substitution.

$\lim \limits_{x \to y} x = \lim \limits_{t \to 1} t^{\frac{1}{t-1}} = \lim \limits_{s \to 0} (1+s)^{\frac{1}{s}} = e$

$\lim \limits_{x \to y} y = \lim \limits_{t \to 1} t^{\frac{t}{t-1}} = \lim \limits_{s \to 0} (1+s)^{\frac{1}{s}+1} = e$

Thus, we can evaluate the limit as

$\lim \limits_{x \to y} x^y = e^e = 15.154...$

We begin by observing the graph of the function $x^{{1}/{x}}$ for $x>0$ .

Differentiating the function and equating to zero gives $x^{{1}/{x}} \left( \frac{1-\ln x}{x^2} \right) = 0 \implies x = e$

We can verify this is the only point of maximum of this function for $x>0$ . Hence, $x^{{1}/{x}}$ is increasing for $0<x<e$ and decreasing for $x>e$ .

We can thus conclude that $\exists \ 0<a<e$ and $b>e$ such that $a^{{1}/{a}} = b^{{1}/{b}} \implies a^b = b^a$ . Moreover, the line segment joining the points on the curve $x^{{1}/{x}}$ at $x=a$ and $x=b$ has zero slope since $x^{{1}/{x}} {\huge |}_{x=a} = x^{{1}/{x}} {\huge |}_{x=b}$ , i.e., have the same y-coordinate.

As the line segment joining $a$ and $b$ is gradually vertically ascended, it ultimately becomes tangent to the curve $x^{{1}/{x}}$ at $x=e$ (as it is the point of maxima). 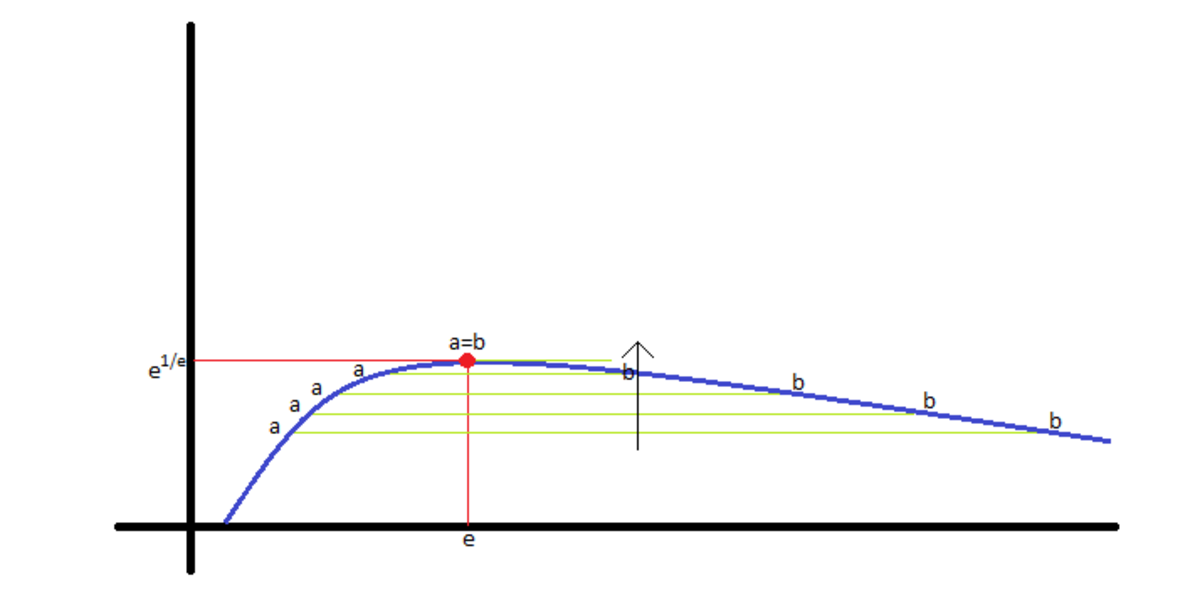This illustration is not the exact graph. Intended just for the sake of reasoning.

Likewise, we conclude in the statement of problem that if $a \to b$ satisfying $a^b = b^a$ then $a \to e, b \to e$ . Hence, the value of the limit is $e^e = \boxed{15.154}$ .