Converging integration series

Calculus Level 3

Prove that the series converges:(See the serie carefully) In the options by e it means Euler Masheroni constant

$1 - \int_1^2 \dfrac {dx}x + \dfrac12 - \int_2^3 \dfrac{dx}x + \dfrac13 - \cdots$

Also find the sum of the expression

1 0 e 2

1 solution

Purnashis Hazra
Jan 17, 2016

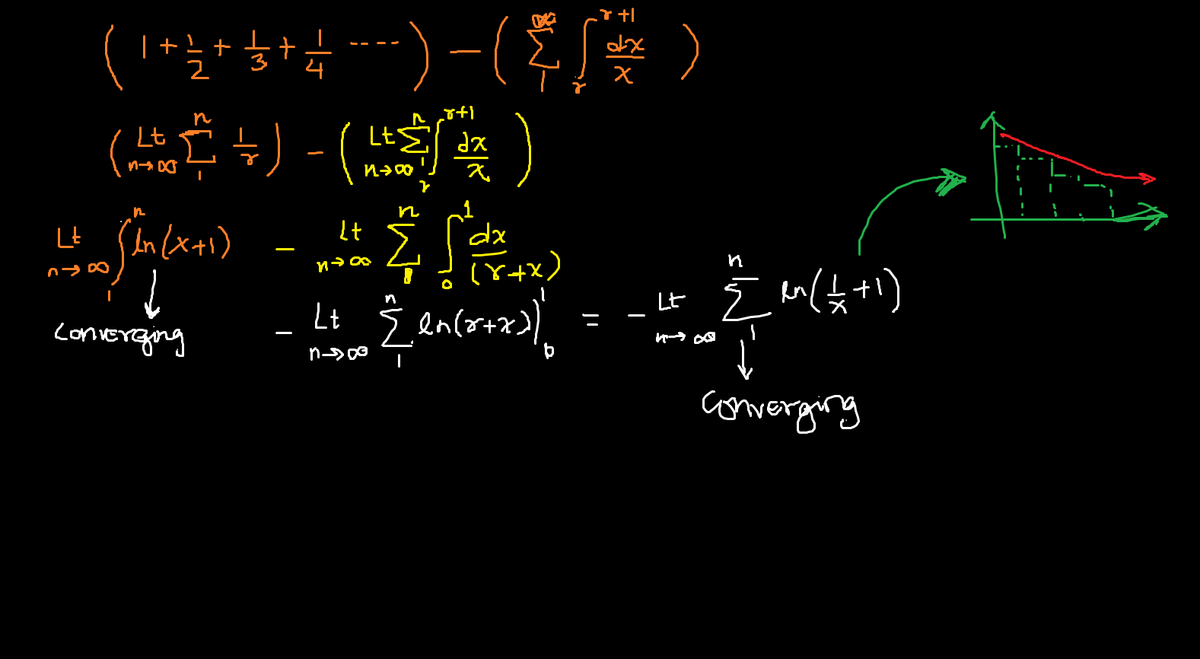
ah no mames, no te pases, te cuesta tanto poner \gamma en vez de e >:v. troll xD

Angel Loquez - 4 years ago

You did not show the proof on how this sum comes to $e$ . In fact, the sum of this is known as Euler–Mascheroni constant, represented with $\gamma$ . In transforming the Harmonic series to logarithm, you ignore its divergence characteristics. Simply put, $lim_{n\rightarrow\infty}\sum_{m=1}^n \frac{1}{m}$ Diverges. However, $\gamma$ , the sum of $lim_{n\rightarrow\infty}(-ln(n)+\sum_{m=1}^n \frac{1}{m})$ Converges to $\gamma \approx 0.5772156$

Kay Xspre - 5 years, 4 months ago

well by e i meant Euler constant as the book i read from showed me e instead of gamma symbol for the same constant but u are right it shouldn't be the same

Purnashis Hazra - 5 years, 4 months ago

Converging integration series

1 solution

0 pending reports