Converging Triangle
Let there be a triangle A 1 A 2 A 3 as shown in figure below. Lines A i A i + 1 are drawn with A i + 1 lying on A i − 1 A i − 2 such that
A i + 1 A i − 1 A i − 2 A i + 1 = 7 3 i ≥ 3 i ∈ N
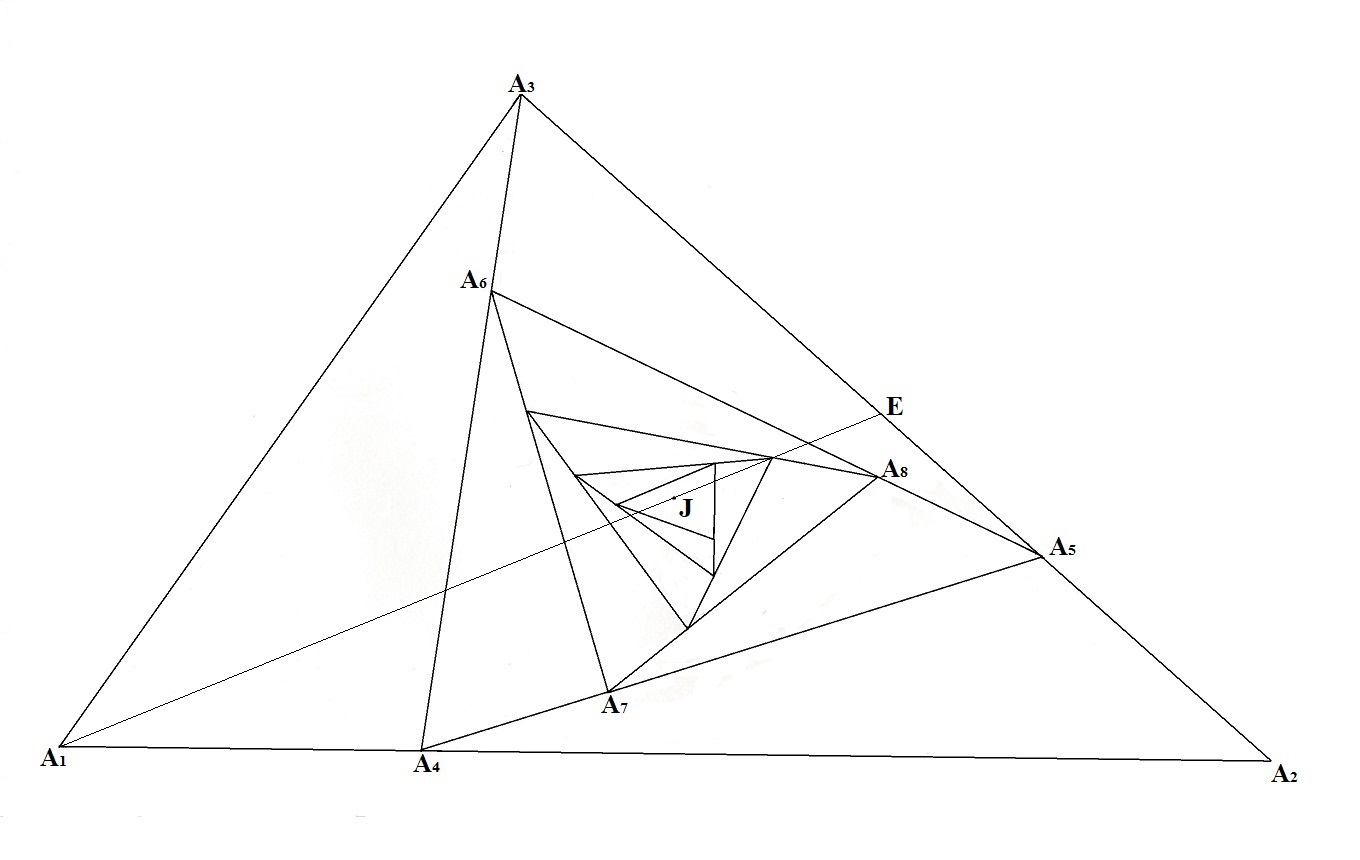
In this way △ A i − 2 A i − 1 A i becomes smaller as i is getting larger and ultimately converges to a point say J . Join A 1 and J and extend it to meet A 2 A 3 at E .
If J E A 1 J = b a where a and b are coprime. Find a + b .
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Please contribute your ideas to one of my notes which is very related to this problem. I have used your approach but not able to proceed after some steps. Link to the note is : Converging Triangle - 2
I was not able to mention you there because your name was not coming in the drop down menu form when I have written your name.
The given condition on the ratio of lengths, implies that
1 0 A i + 1 = 7 A i − 2 + 3 A i − 1 ( 1 ) , which can be written as
1 0 A i + 3 − 3 A i + 1 − 7 A i = 0 , i = 1 , 2 , . . . ( 2 )
This is a difference equation of order 3, its characteristic polynomial is 1 0 m 3 − 3 m − 7 = 0 , which by inspection has a root at m = 1 , so dividing it by ( m − 1 ) using synthetic division results in 1 0 m 3 − 3 m − 7 = ( m − 1 ) ( 1 0 m 2 + 1 0 m + 7 ) = 0 . The quadratic has the roots m = − 2 1 ± i 1 0 3 5 . It follows from this and from standard difference equation solution methods, that
A k = P + Q a ( k − 1 ) cos ( ω ( k − 1 ) ) + R a ( k − 1 ) sin ( ω ( k − 1 ) ) ( 3 )
where a = ∣ m ∣ = 0 . 7 and ω = tan − 1 5 3 , and P , Q , and R are two dimensional vectors. Obviously since ∣ a ∣ < 1 , the only vector that matters is P , as the contribution of Q and P will die out. To solve for P , we can write,
[ A 1 , A 2 , A 3 ] = [ P , Q , R ] M ( 4 )
where M is the following 3 × 3 matrix (this is can be seen from equation (3) after substituting k = 1 , 2 , 3
M = ⎣ ⎡ 1 1 0 1 a cos ω a sin ω 1 a 2 cos 2 ω a 2 sin 2 ω ⎦ ⎤ ( 5 )
From (4), we now have,
[ P , Q , R ] = [ A 1 , A 2 , A 3 ] M − 1 ( 6 )
The inverse of M can be found using any standard mathematical tool. Note that we only care about the first column of M − 1 , and this column is given by,
M − 1 ( ⋅ , 1 ) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 2 7 7 2 7 1 0 2 7 1 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ( 7 )
So that, P = J = 2 7 7 A 1 + 2 7 1 0 ( A 2 + A 3 ) ( 8 )
From this it follows that points on the line A 1 J are given by A 1 + s ( A 1 J ) = A 1 + s ( J − A 1 ) = A 1 + s ( − 2 7 2 0 A 1 + 2 7 1 0 ( A 2 + A 3 ) )
The point E depends only on A 2 and A 3 , so the value of s at point E is 2 0 2 7 , and therefore, finally, the required ratio is
Ratio = 2 0 2 7 − 1 1 = 2 0 7 1 = 7 2 0
Making the answer 2 0 + 7 = 2 7
Putting i = 3
In △ A 1 A 2 A 3 , A 4 is a point on A 1 A 2 such that A 4 A 2 A 1 A 4 = 7 3
This pattern is continued for i ≥ 4 and we will get a point J which is the converging point of △ A i − 2 A i − 1 A i for i → ∞ .
Join A 3 and J and extend it to meet A 1 A 2 at F 3 .
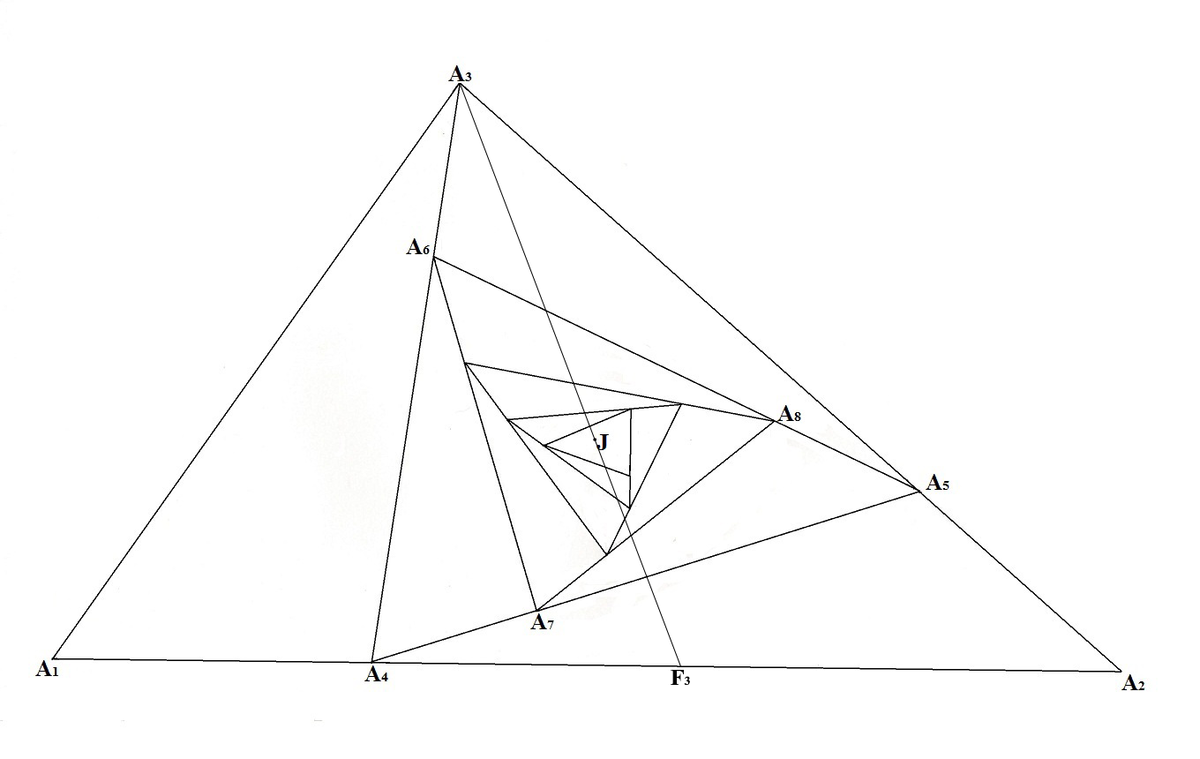
Now taking one extra case of i = 2 and assuming some point A 0 in the plane of figure. According to question, we will have a line A 2 A 3 with A 3 lying on line A 0 A 1 such that
A 3 A 1 A 0 A 3 = 7 3 ⋯ E q . 1
That means A 0 lies on A 1 A 3 extended and located such that E q . 1 holds. Join A 2 and A 0 . Join A 2 and J and extend it to meet A 1 A 3 at F 2 . This is illustrated in figure below.
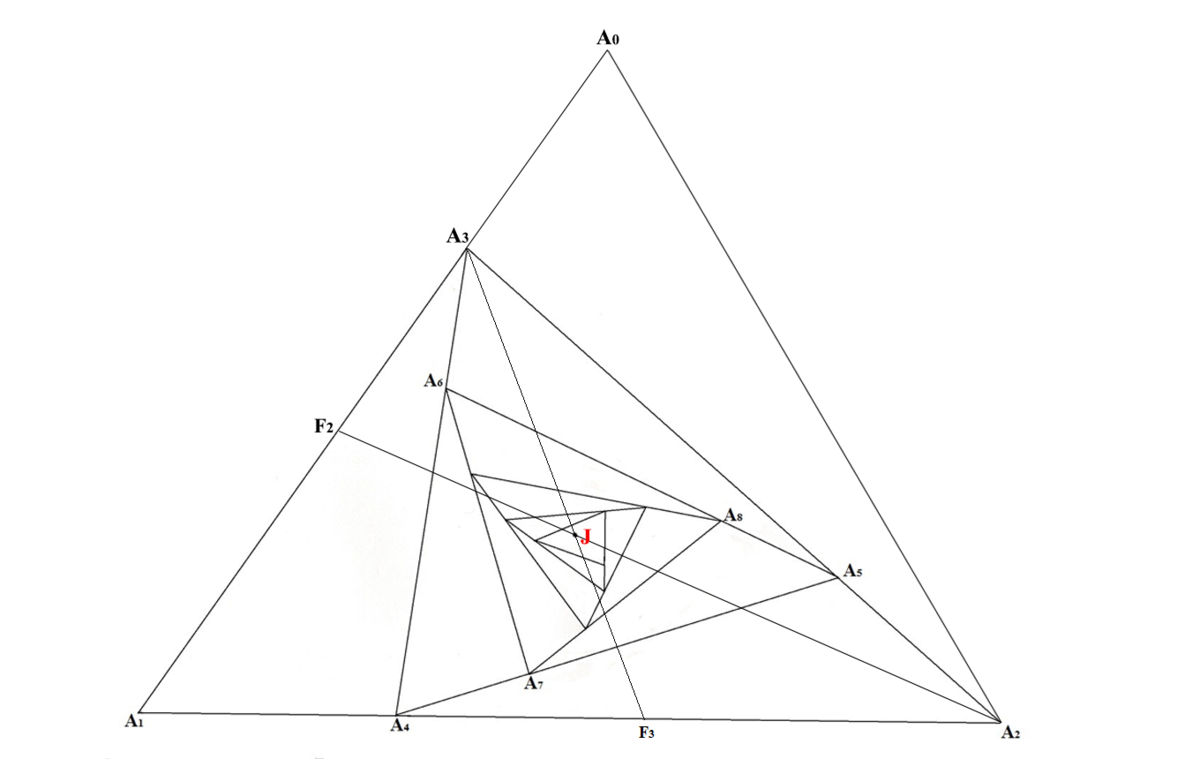
We see that adding one extra point A 0 or in fact, forming a new △ A 0 A 1 A 2 does not affect the position of J . So we can conclude that △ A 0 A 1 A 2 is analogous to △ A 1 A 2 A 3 if we take the starting triangle as △ A 0 A 1 A 2 . So, line A 2 J F 2 is analogous to line A 3 J F 3 .
So, J F 2 A 2 J = J F 3 A 3 J ⋯ E q . 2
It can be easily prove that because of E q . 2 , J lies on median of △ A 1 A 2 A 3 through A 1 . I am skipping this proof.
Join A 1 and J and extend it to meet A 2 A 3 at E . Then E is the mid-point of A 2 A 3 .
In the similar manner taking i = 4 we get △ A 2 A 3 A 4 analogous to △ A 1 A 2 A 3 and also line A 4 J F 4 analogous to line A 3 J F 3 .
So, J F 4 A 4 J = J F 3 A 3 J ⋯ E q . 3
Again, because of E q . 3 , J lies on median of △ A 2 A 3 A 4 through A 2 . which coincides with the line A 2 J F 2 .
Let this line intersect A 3 A 4 at H . Then H is the mid-point of A 3 A 4 .
Thus, location of J can be defined as the intersection point of two lines A 1 E and A 2 H where E and H are the mid-point of A 2 A 3 and A 3 A 4 respectively. This is shown in figure below.
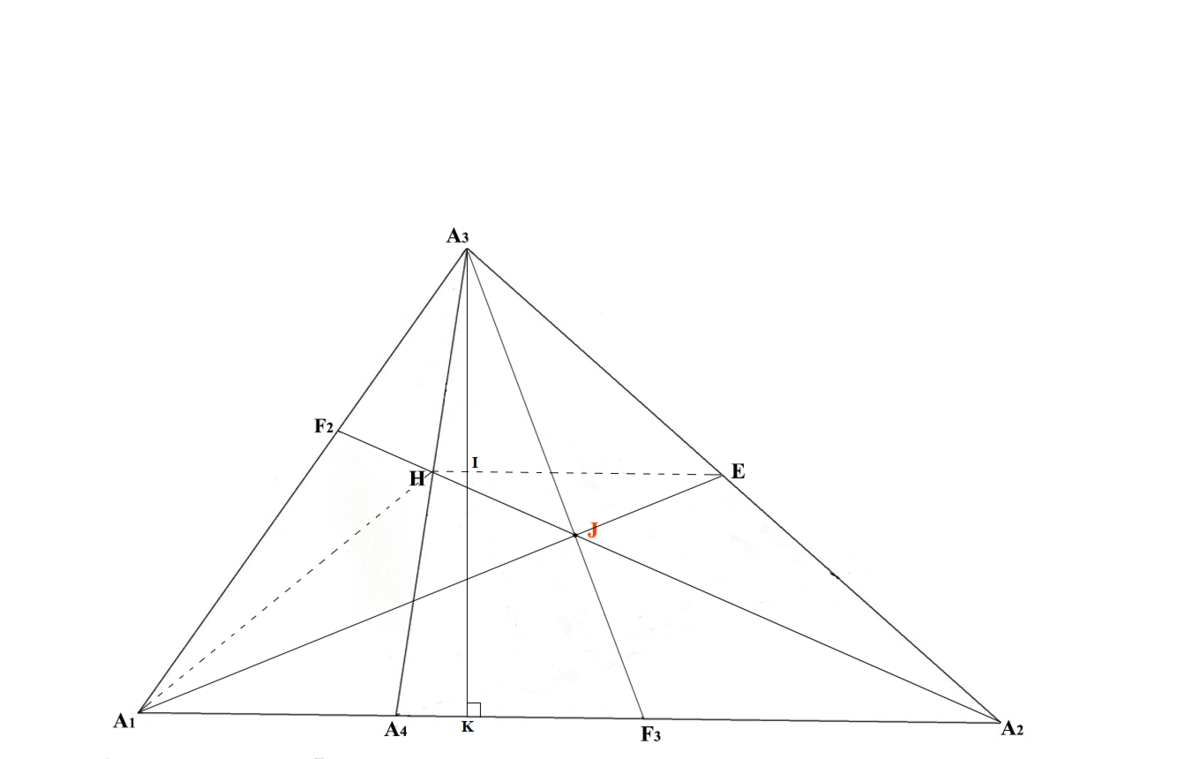
Let area of △ A 1 A 2 A 3 be X . Further in the solution below, area of any triangle P Q R will be denoted by a r ( △ P Q R ) .
I have frequently used the property of the triangle that the area of triangles between the same parallels are in the proportions of their base.
a r ( △ A 3 A 1 A 4 ) a r ( △ A 3 A 1 A 2 ) = A 1 A 4 A 1 A 2 = A 1 A 4 A 1 A 4 + A 4 A 2 = 1 + 3 7 = 3 1 0
⇒ a r ( △ A 3 A 1 A 4 ) = 1 0 3 X
⇒ a r ( △ A 3 A 4 A 2 ) = X − 1 0 3 X = 1 0 7 X
⇒ a r ( △ A 3 A 4 A 2 ) a r ( △ A 3 H A 2 ) = 2 1
⇒ a r ( △ A 3 H A 2 ) = 2 1 ⋅ a r ( △ A 3 A 4 A 2 ) = 2 1 ⋅ 1 0 7 X = 2 0 7 X ⋯ E q . 4
⇒ a r ( △ A 1 H A 2 ) = a r ( △ A 1 E A 2 ) = 2 1 ⋅ a r ( △ A 3 A 1 A 2 ) = 2 X ⋯ E q . 5 [ ∵ H , E are the mid-points of A 3 A 4 and A 3 A 2 ⇒ H E ∥ A 1 A 2 ]
Now, F 2 A 1 A 3 F 2 = a r ( △ A 1 F 2 A 2 ) a r ( △ A 3 F 2 A 2 ) = a r ( △ A 1 F 2 H ) a r ( △ A 3 F 2 H ) = a r ( △ A 1 F 2 A 2 ) − a r ( △ A 1 F 2 H ) a r ( △ A 3 F 2 A 2 ) − a r ( △ A 3 F 2 H ) = a r ( △ A 1 H A 2 ) a r ( △ A 3 H A 2 ) = 2 X 2 0 7 X = 1 0 7 ⋯ E q . 6 [ From E q . 4 and E q . 5 ]
Also, F 2 A 1 A 3 F 2 = a r ( △ A 1 F 2 A 2 ) a r ( △ A 3 F 2 A 2 ) = a r ( △ A 1 F 2 J ) a r ( △ A 3 F 2 J ) = a r ( △ A 1 F 2 A 2 ) − a r ( △ A 1 F 2 J ) a r ( △ A 3 F 2 A 2 ) − a r ( △ A 3 F 2 J ) = a r ( △ A 1 J A 2 ) a r ( △ A 3 J A 2 )
⇒ a r ( △ A 1 J A 2 ) a r ( △ A 3 J A 2 ) = F 2 A 1 A 3 F 2 = 1 0 7 [ From E q . 6 ]
⇒ a r ( △ A 1 J A 2 ) 2 ⋅ a r ( △ E J A 2 ) = 1 0 7 [ ∵ a r ( △ E J A 2 ) a r ( △ A 3 J A 2 ) = 2 ]
⇒ a r ( △ A 1 J A 2 ) a r ( △ E J A 2 ) = 2 0 7
Now, J E A 1 J = a r ( △ E J A 2 ) a r ( △ A 1 J A 2 ) = 7 2 0
So, the answer is 2 0 + 7 = 2 7
Say point A n has coordinates ( x n , y n ) . We have
1 0 x n + 3 = 3 x n + 1 + 7 x n and 1 0 y n + 3 = 3 y n + 1 + 7 y n
Since we can treat x i and y i independently, we will look at the general solution of the recurrence relation 1 0 u n + 3 = 3 u n + 1 + 7 u n .
The characteristic equation of this recurrence relation is 1 0 t 3 = 3 t + 7 . This has a real root at t = 1 and two complex roots t = 1 0 1 ( − 5 ± 3 i 5 ) (the complex roots correspond to the spiralling behaviour of the points).
In order to find point J , we want to know the long-term behaviour of u n given three initial points.
Put τ = 1 0 1 ( − 5 + 3 i 5 ) . The general solution of the recurrence relation is
u n = P + Q τ n + Q τ n
(where z is the complex conjugate of z . We know we can use the conjugate this way because we are dealing with real values for the coordinates)
Since ∣ τ ∣ < 1 , as n → ∞ , u n → P .
So the problem boils down to finding the value of P from the initial points. Here we can save some effort by using a couple of tricks.
We could at this point solve completely generally; however, we can note that changing the initial triangle won't in fact change the ratio we are looking to find. This means we can pick a "nice" triangle and solve for that.
Further, let's relabel the vertices so that instead of starting at n = 1 , we start at n = 0 . This has the effect of slightly simplifying the algebra when working out P .
Let's choose the starting triangle A 0 ( 0 , 0 ) , A 1 ( 1 , 0 ) , A 2 ( 0 , 1 ) . This triangle has the benefit of satisfying y n = x n − 1 (simple to check), so J lies on the line y = x , and we only need to solve for x n . Since E is the intersection of the lines A 0 J and A 1 A 2 , we have E ( 2 1 , 2 1 ) .
We still have to find J , however.
The three starting points give us the simultaneous equations
P + Q + Q = 0 P + Q τ + Q τ = 1 P + Q τ 2 + Q τ 2 = 0
Solving these, we find P = 2 7 1 0 , and so we have J ( 2 7 1 0 , 2 7 1 0 ) .
Finally, by similar triangles (one last trick!), we simply have J E A 0 J = 2 1 − 2 7 1 0 2 7 1 0 = 7 2 0 giving the answer 2 0 + 7 = 2 7 .