Conversion of volume

Geometry Level 2

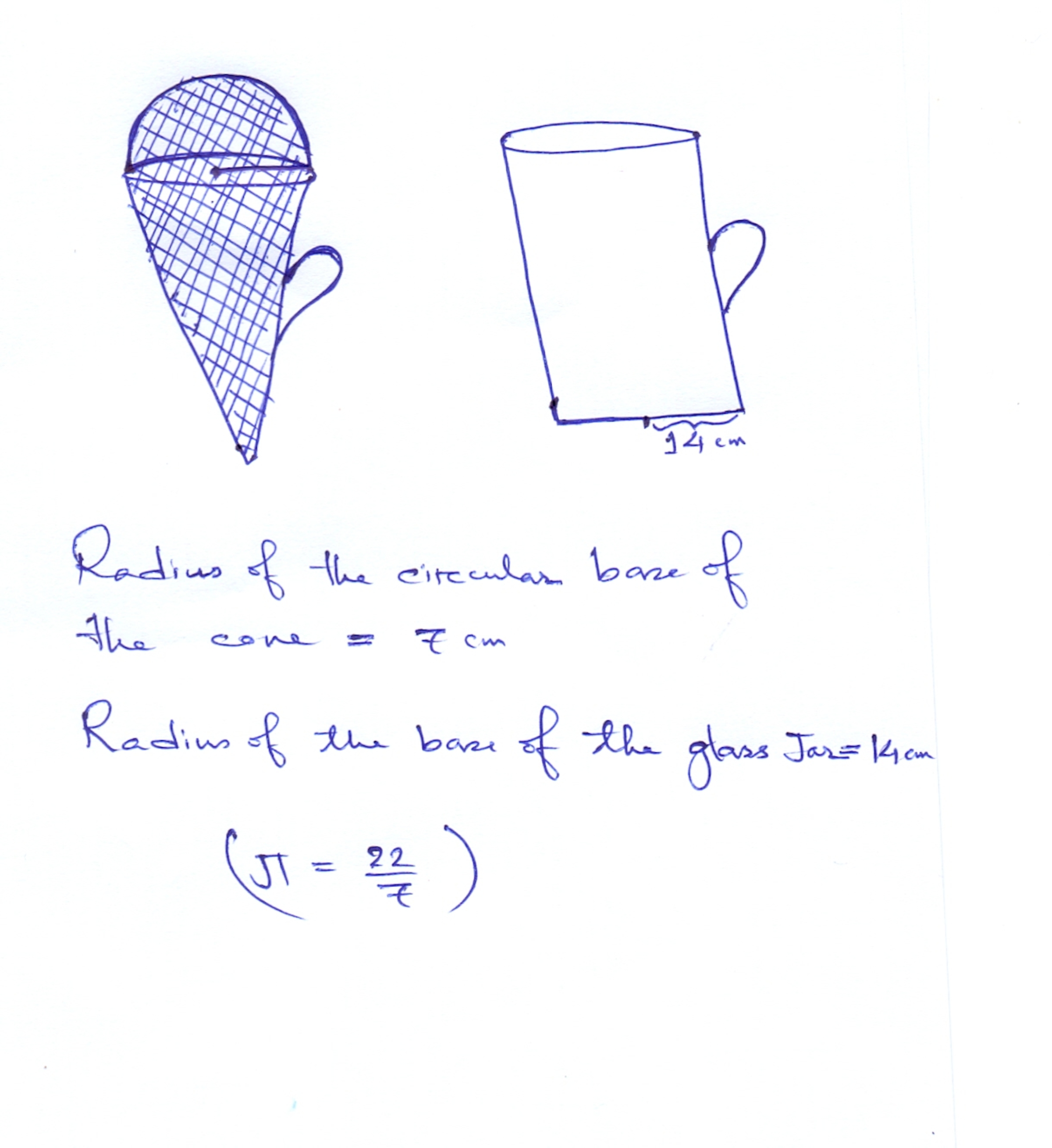
The entire ice cream from the cone is poured in the Glass jar. Find the height of the ice cream within the Right circular Jar.

Take pi=22/7.
Height of the cone is 9cm and radius of the base is 7cm.
Radius of the circular base of the glass jar is 14cm. Assume that temperature of the ice cream remains the same during transfer.


The answer is 1.92.

Dinamani Borah by Dinamani Borah , 42, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The volume of the ice cream is equal to the volume of the right circular cone plus the volume of the hemisphere. We have

V i c e c r e a m = 1 3 ( π ) ( r 2 ) ( h ) + ( 1 2 ) ( 4 3 ) ( π ) ( r 3 ) = 1 3 ( 22 7 ) ( 7 2 ) ( 9 ) + 2 3 ( 22 7 ) ( 7 3 ) = 462 + 2156 3 = 3543 3 V_{ice~cream}=\dfrac{1}{3}(\pi)(r^2)(h)+\left(\dfrac{1}{2}\right)\left(\dfrac{4}{3}\right)(\pi)(r^3)=\dfrac{1}{3}\left(\dfrac{22}{7}\right)(7^2)(9)+\dfrac{2}{3}\left(\dfrac{22}{7}\right)(7^3)=462+\dfrac{2156}{3}=\dfrac{3543}{3}

The above volume must also be the volume of ice-cream in the right circular jar. So

3543 3 = π ( r 2 ) ( h ) \dfrac{3543}{3}=\pi(r^2)(h)

3543 3 = 22 7 ( 1 4 2 ) ( h ) \dfrac{3543}{3}=\dfrac{22}{7}(14^2)(h)

h = 1.917 c m \color{#D61F06}\boxed{h=1.917~cm}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...