G.R.O.S.S
 In how many ways can 4 boys (A, B, C, D) and 4 girls (W, X, Y, Z) be seated in a row, such that all the girls do not sit together?
In how many ways can 4 boys (A, B, C, D) and 4 girls (W, X, Y, Z) be seated in a row, such that all the girls do not sit together?
The answer is 37440.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
Let's first calculate the number of ways the kids can be seated without any restriction; this is simply P 8 = 8 ! = 4 0 3 2 0
Now, if all girls are seated together, then we can consider them as "one girl" to determine the ways they can seat together with the remaining four boys; this is equal to P 5 = 5 ! = 1 2 0 . This, however, doesn't cover all of the possibilities, because the girls can be sitting together in P 4 = 4 ! = 2 4 different ways; thus, we have to multiply them both to get all of the possibilities which involve the girls sitting together: P 5 ∗ P 4 = 5 ! ∗ 4 ! = 2 8 8 0 .
Thus, the total of possibilities we want is the difference between all of the possibilities and what we don't want to happen. Simply stated, this is: 4 0 3 2 0 − 2 8 8 0 = 3 7 4 4 0 .
When all girls are seated together, then we can consider them as "one pack", and
this pack has 5 places
P B P B P B P B P
The number of ways the 4 girls can be seated together in the pack = 4!
The number of ways the pack can be seated with the remaining 4 boys = 5
The number of ways the 4 boys can be sit with the pack = 4!
Then
The number of ways the 4 girls can be seated together = (4!)(5)(4!) = (4!)(5!)
NOW
The number of ways the 8 kids can be sit in a row = 8!
The number of ways the boys and girls can be seated in a row, such that all the
girls do not sit together = 8! - (4!)(5!) = 37440
total ways of arranging are 8!
ways in which all girls can sit together: for this consider all the girls as single point as they can not get separated. thus total members can be considered as five. the probability is 5!*4!.( 4! is added because for each arrangement girls can further arrange arrange themselves in 4! ways.)
thus the possible ways that girls are never seated together are: (Total ways-girls seated together) =8!-(5!*4!) =37440
There are only 5 combinations of seats where all the girls can be seated all together and they can be seated 4! ways in each combination. The boys can also be seated 4! ways in the remaining seats. Thus, the number of ways girls can be seated all together is (5)(4!)(4!). 8! is number of ways all of the boys and girls can be seated without restriction. So what we want is 8!-5(4!)(4!)=37440.
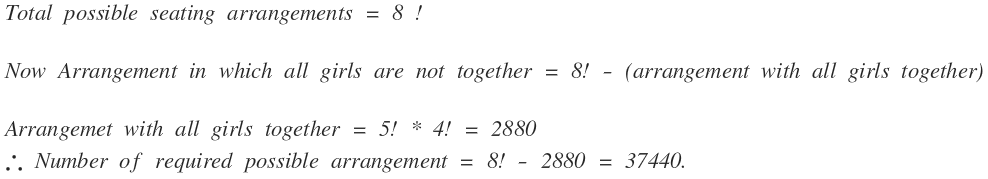
The total possible ways of the arrangment of sitting : 8 P 8 (P=>permutation) =8!
Ways in which all the girls sit together are:5 P 5 * 4! = 5!*4!
5 P 5 =>assuming all the girls as 1 single
4!=>ways in which the girls can change their seats among themselves
Therefore the answer is: 8! - (5!*4!) = 37440