Cool distribution on a circumference

The worst scenario is when the points are evenly distributed. Then the angle between two points is $60^\circ$ , so the arc containing all has to be $360^\circ-60^\circ=\boxed{300^\circ}$ .

DISCLAIMER: This is a very similar proof to @Marta Reece , but with a visual aspect.

First, we must figure out how to solve for $n=2$ . Then, we can understand how to solve for $n=6$ We can generalize this, later!

Since we want an arc to contain all possible points, we need to have an example where the points are as spread out as possible. For $n=2$ , this means they would be opposite of each other:

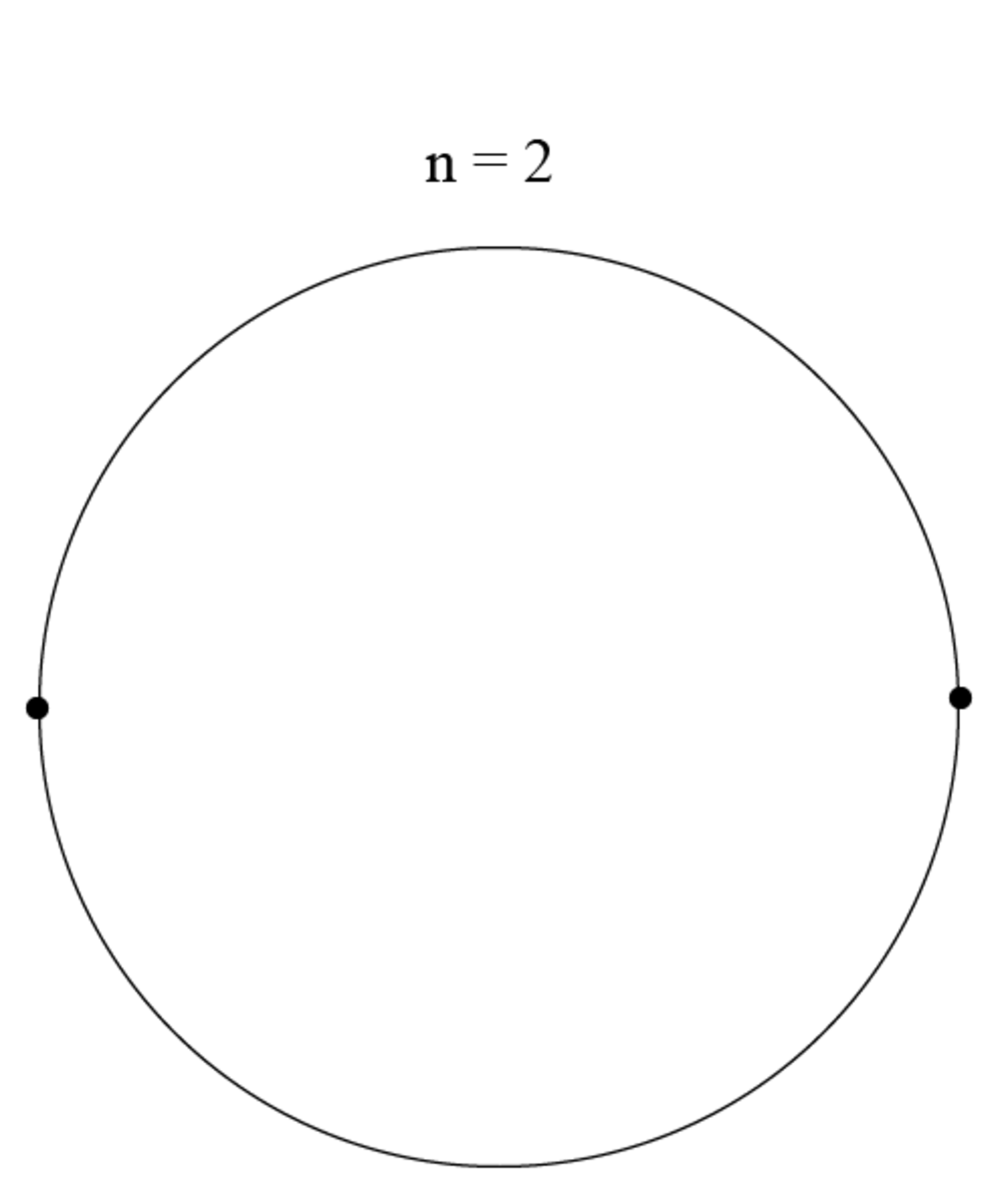
Since we need half a circle, the answer would be 180°.

Now, we can solve for $n=6$ .

In order to have all 6 points as spread out as possible, we could label the points as the vertices of a regular hexagon inscribed in a circle:

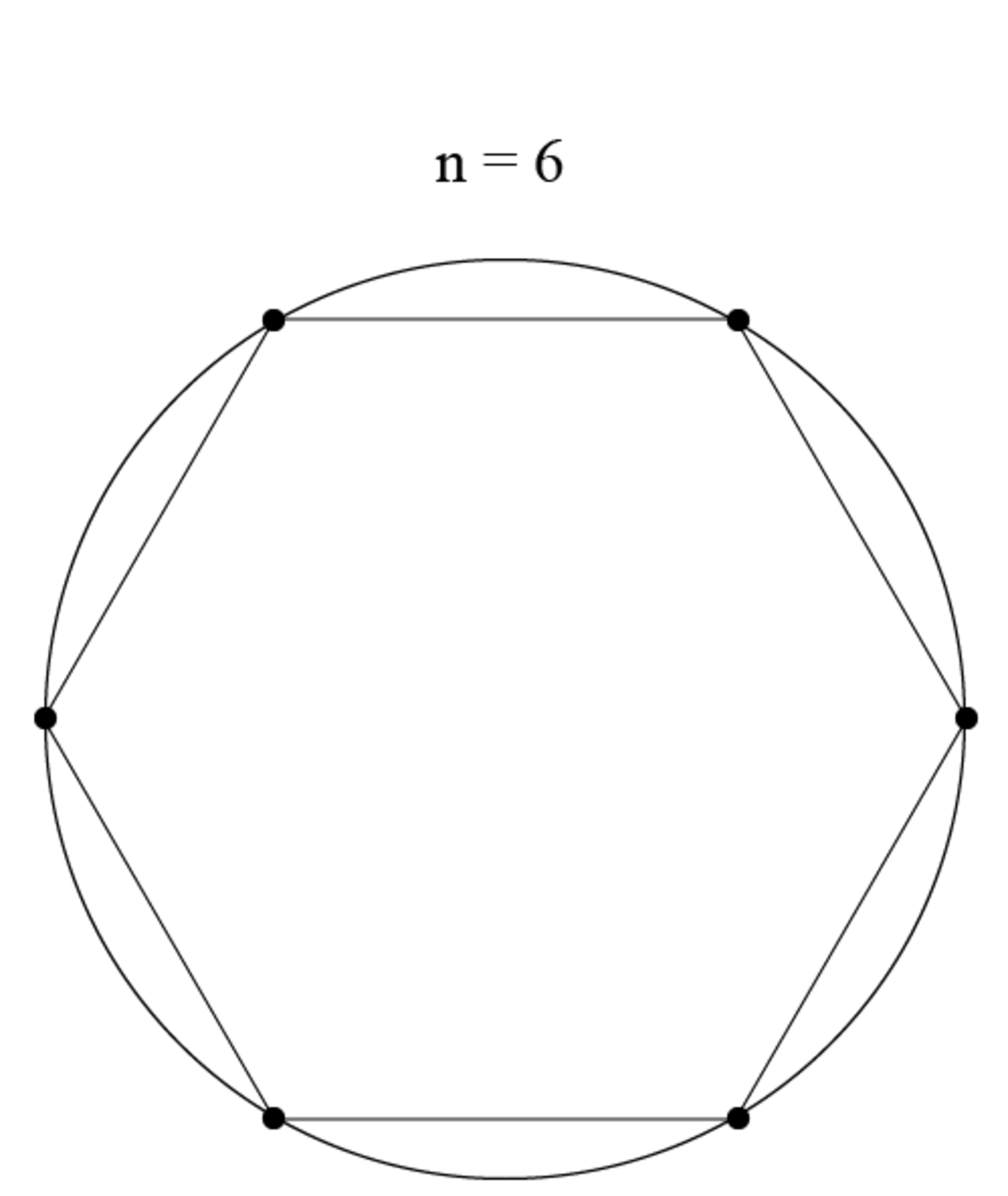
Since $\frac{1}{6}^{\text{th}}$ of the circle is between each of the points, that means that there must be $\frac{360}{6}$ = 60° between each point on the circle:

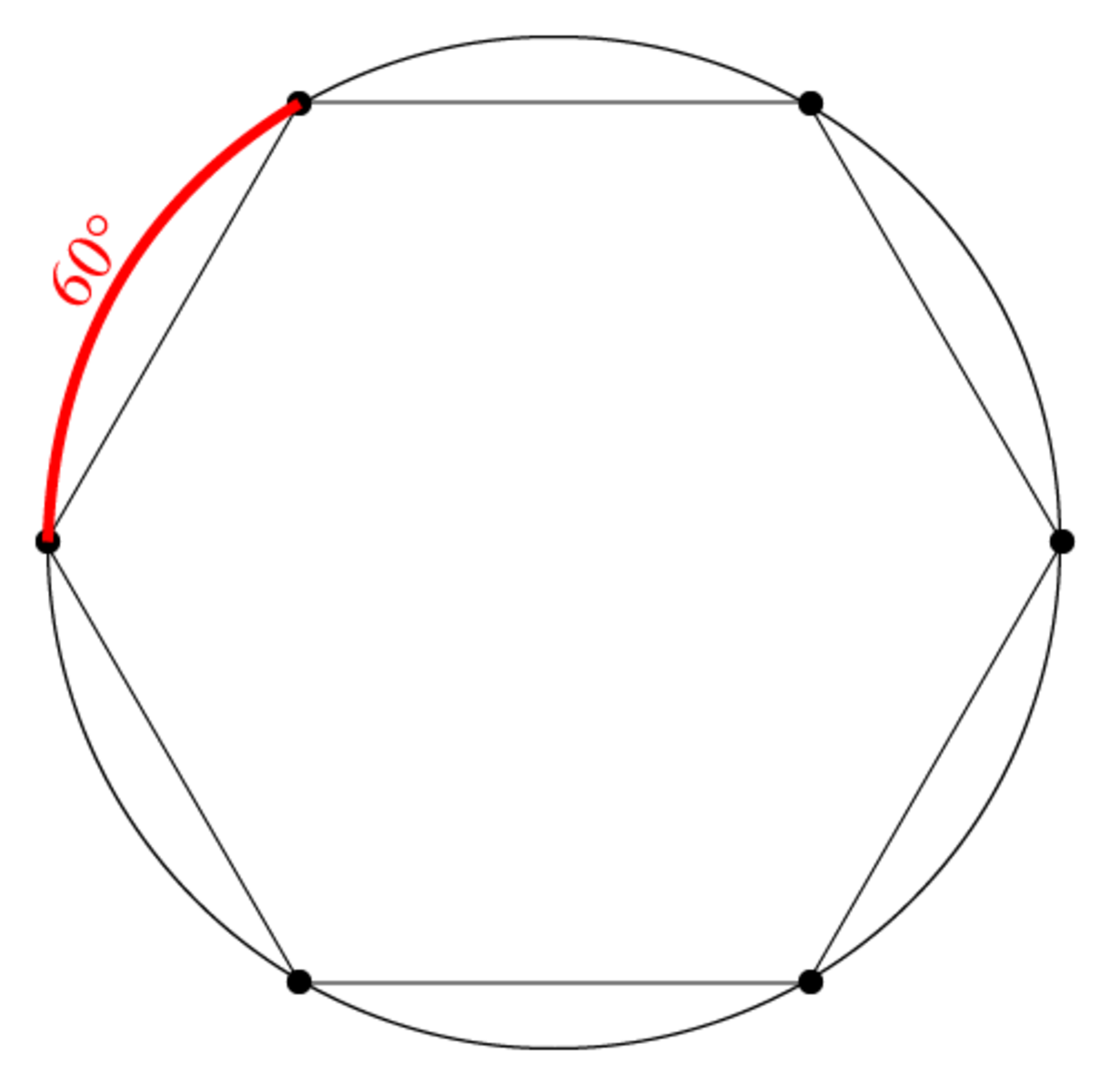
The black arc covers all of the points, so the red arc can be subtracted from the circle, to get $360-60=\boxed{300}$

Now, we can generalize for $n$ . We can think of inscribing a regular polygon with $n$ sides inside a circle, with each of the vertices as a point on the circle. We can subtract one of the arcs made by two adjacent points. The arc between two adjacent points would be $\frac{360}{n}$ . Therefore, the maximum central angle necessary to contain $n$ points on a circle would be represented as $360-\frac{360}{n}$ .