Cool distribution on a circumference #2

Any point $P$ on the circle defines a semicircle $S_P$ , starting at that point, and moving anticlockwise around the circle. A collection $P_1,P_2,...,P_n$ of $n$ points form a polygon which does not contain the centre precisely when they all lie in some semicircle, and so must lie in one of the semicircles $S_{P_j}$ . The events $A_1,A_2,...,A_n$ , where $A_j$ is the event that all points lie in $S_{P_j}$ are mutually exclusive, and the probability of each $A_j$ is $\big(\tfrac12\big)^{n-1}$ . Thus the probability $p_n$ that the $n$ points form a polygon that does not contain the centre of the circle is $p_n \; = \; P[A_1 \cup A_2 \cup \cdots \cup A_n] \; = \; \frac{n}{2^{n-1}}$ We are therefore interested in the two conditional probabilities $A \; = \; 1 - \frac{p_4}{p_3} \; = \; \tfrac13 \hspace{2cm} B \; = \; 1 - \frac{p_5}{p_4} \; =\; \tfrac38$ making the answer $AB = \tfrac18 = \boxed{0.125}$ .

The question is equivalent to:

$1.$ Picking a point on the circle

$2.$ Picking $n-2$ points on one half of the circle, uniformly at random. (This ensures the $n-1-\text{gon}$ doesn't contain the center.)

$3.$ Asking for the maximal expected distance, $X_{n-1}$ , along the circle between two of these $n-1$ points (and dividing that by $2\pi$ ).

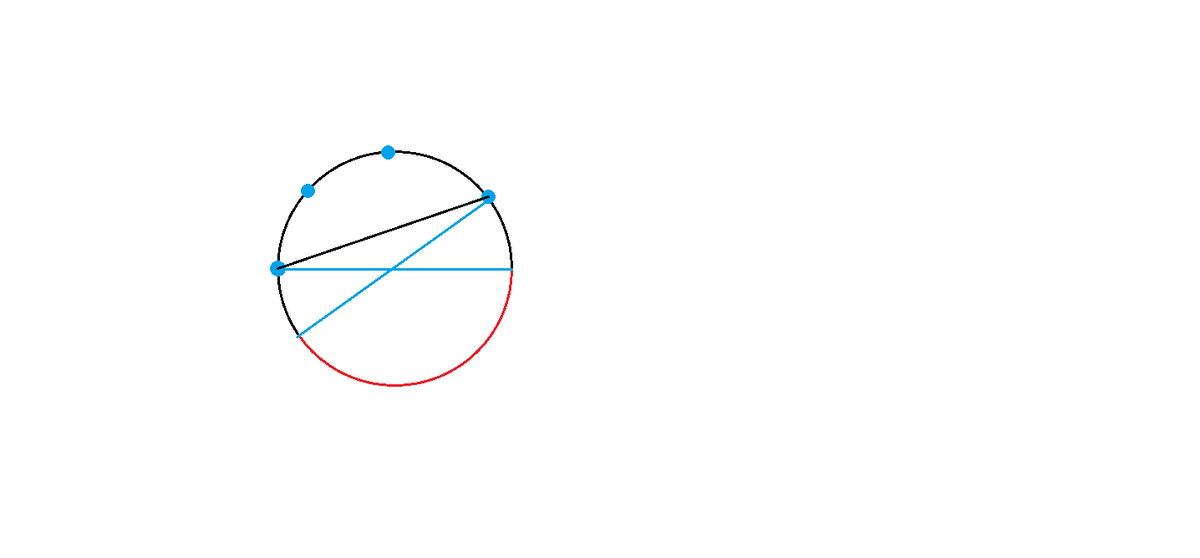$\text{In the image, there are } n-1=4 \text{ points already selected. In order for the center to be within the }n\text{-gon, the } n \text{-th point must be on the red segment.}$

Finding $X_n$ is easy: the probability the answer is $x$ is $\displaystyle P(x)=n\cdot(\frac{x}{\pi})^{n-1}\cdot\frac{dx}{\pi}$ , so:

$X_n=\displaystyle\int_{0}^{\pi}x\cdot P(x)=\frac{1}{\pi^n}\int_{0}^{\pi}n\cdot x^n\cdot dx=\frac{\pi\cdot n}{n+1}$

making the answer $\displaystyle\frac{X_2}{2\pi}\cdot\frac{X_3}{2\pi}=\frac{2\cdot3}{6\cdot8}=\frac{1}{8}$ .

a) The central angle that 4 points can form on a circumference is at most $270º$ .

3 points have been placed independently and randomly on a circumference, and it is known that the triangle formed by the 3 points does not contain the center of the circle, and a fourth point has been placed independently of the other 3 points and randomly on the circumference. This implies that the 3 first points form a central angle less than $180º$ Hence, we have two possibilities:

1.- the 4 points form a quadrilateral that doesn't contain the center of the circle. So, the four points keep on forming a central angle less than $180º$ and the probability for this happenning is $\frac{180}{270} = \frac{2}{3}$

2.- the 4 points form a quadrilateral that contains the center of the circle. Then, $A = \frac{270 - 180}{270} = \frac{1}{3}$ .

b) With the same reasoning $B = \frac{288 - 180}{288} = \frac{3}{8}$ and $A \cdot B = \frac{1}{8} = 0.125$

---

Generalization.-

$\boxed{1.-}$ The probability for that the triangle formed by 3 points placed independently, uniformly and randomly on a circumference does not contain the center of the circle is $\frac{3}{4} = \frac{180}{240} \Rightarrow$ the probability for that the triangle formed by 3 points placed independently, uniformly and randomly on a circumference contains the center of the circle is $\frac{1}{4} = \frac{240 - 180}{240} = 1 - \frac{3}{4}$ .

$\boxed{2.-}$ The probability for that the quadrilateral formed by 4 points placed independently, uniformly and randomly on a circumference does not contain the center of the circle is $\frac{1}{2} = \frac{3}{4} \cdot \frac{2}{3} = \frac{3}{4} \cdot \frac{180}{270} \Rightarrow$ the probability for that the quadrilateral formed by 4 points placed independently, uniformly and randomly on a circumference contains the center of the circle is $\frac{1}{2} = 1 - \frac{1}{2} = \frac{1}{4} + \frac{3}{4} \cdot \frac{270 - 180}{270} = \frac{1}{4} \cdot 1 + \frac{3}{4} \cdot \frac{1}{3}$ .

To be continued...