Cool Geometry

Geometry Level 3

In △ A B C \triangle ABC , ∠ A = 2 ∠ B \angle A=2\angle B . What is the value of B C 2 BC^{2} ?

3 A C − A B 3AC-AB None of these A C ( A C + A B ) AC(AC+AB) A B 2 AB^{2} A B + A C AB+AC

View wiki
Aditya Lalbondre by Aditya Lalbondre , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Extend C A CA to D D Such that ∠ C B D = ∠ C A B \angle CBD=\angle CAB

△ C B A \triangle CBA is similar to △ C D B \triangle CDB

C B C D \frac{CB}{CD} = C A C B \frac{CA}{CB}

So,

B C 2 = C D ⋅ C A BC^{2}=CD \cdot CA

Also,

A B = A D AB=AD ..........................Isoceles triangle theorem in △ B A D \triangle BAD

So,

B C 2 = A C ( A C + A B ) BC^{2}=AC(AC+AB)

16 Helpful 2 Interesting 2 Brilliant 2 Confused

It's an rmo problem

Aarush Priyankaj - 2 years, 9 months ago

How is AB = AD?

Shubhrajit Sadhukhan - 7 months ago
Timoy Cheng
Apr 15, 2015

You can use a combination of the law of cosines and law of sines.

Let the length of AB = c, the length of BC = a, the length of AC = b, the measure of angle B be x, and the measure of angle A be 2x.

By the Law of Sines,

sin(A)/sin(B) = sin(2x)/sinx = 2 cosx = a/b

We get:

2cosx = a/b (equation 1)

However, the Law of Cosines states that

cos(B)

= cos x

= (a^2 + c^2 - b^2)/2ac

Substituting this into equation 1, we get the equation

(a^2 + c^2 - b^2)/ac = a/b

(a^2)b + (c^2)b - b^3 = (a^2)c

(a^2)b - (a^2)c = b^3 - (c^2)b

(a^2)(b-c) = b(b^2 - c^2) = b (b+c)(b-c)

(a^2 - b(b+c))(b-c) = 0

So it's either a^2 = b(b+c) (or BC^2 = AC(AC+AB)) or b - c = 0

If b - c = 0, or b = c, then we get that the triangle would be a 45-45-90 triangle, with AC and BC as the legs (using the Law of Sines). Using the Pythagorean theorem, we arrive at BC^2 = AC^2 + AB^2 = AC(AC+AB) (since AB = AC).

Thus, BC^2 = AC(AC+AB)

2 Helpful 1 Interesting 1 Brilliant 0 Confused

In latex:

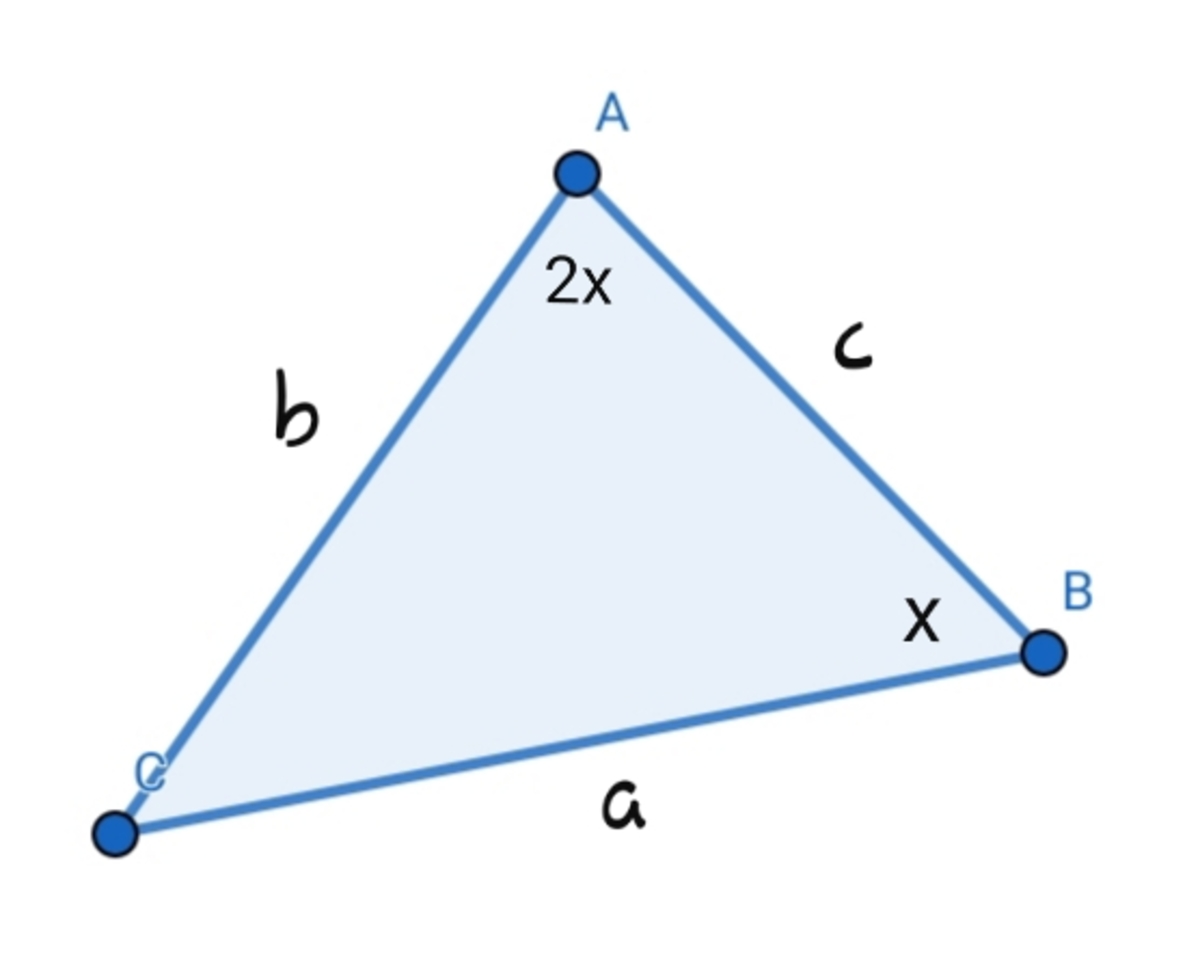
From Cosine rule, b 2 = a 2 + c 2 − 2 a c cos ⁡ x b^2 = a^2 + c^2 - 2ac \cos x cos ⁡ x = a 2 + c 2 − b 2 2 a c \textcolor{#624F41}{\cos x} = \dfrac{a^2 + c^2 - b^2}{2ac}

Using Sine rule, a sin ⁡ 2 x = b sin ⁡ x \dfrac{a}{\sin 2x} = \dfrac{b}{\sin x} a b = sin ⁡ 2 x sin ⁡ x \dfrac{a}{b} = \dfrac{\sin 2x}{\sin x} a b = 2 cos ⁡ x \dfrac{a}{b} = 2 \textcolor{#624F41}{\cos x} a b = 2 ( a 2 + c 2 − b 2 2 a c ) \dfrac{a}{b} = 2 \left(\dfrac{a^2 + c^2 - b^2}{2ac}\right) a 2 c = a 2 b + c 2 b − b 3 a^2c = a^2b + c^2b - b^3 a 2 c − a 2 b = c 2 b − b 3 a^2c - a^2b = c^2b - b^3 a 2 ( c − b ) = b ( c 2 − b 2 ) a^2(c - b) = b(c^2 - b^2) a 2 = b ( c + b ) \boxed{a^2 = b(c + b)} Or, c − b = 0 c - b = 0 that makes the triangle isosceles and right angled, satisfying the required conditions.

Shubhrajit Sadhukhan - 7 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...