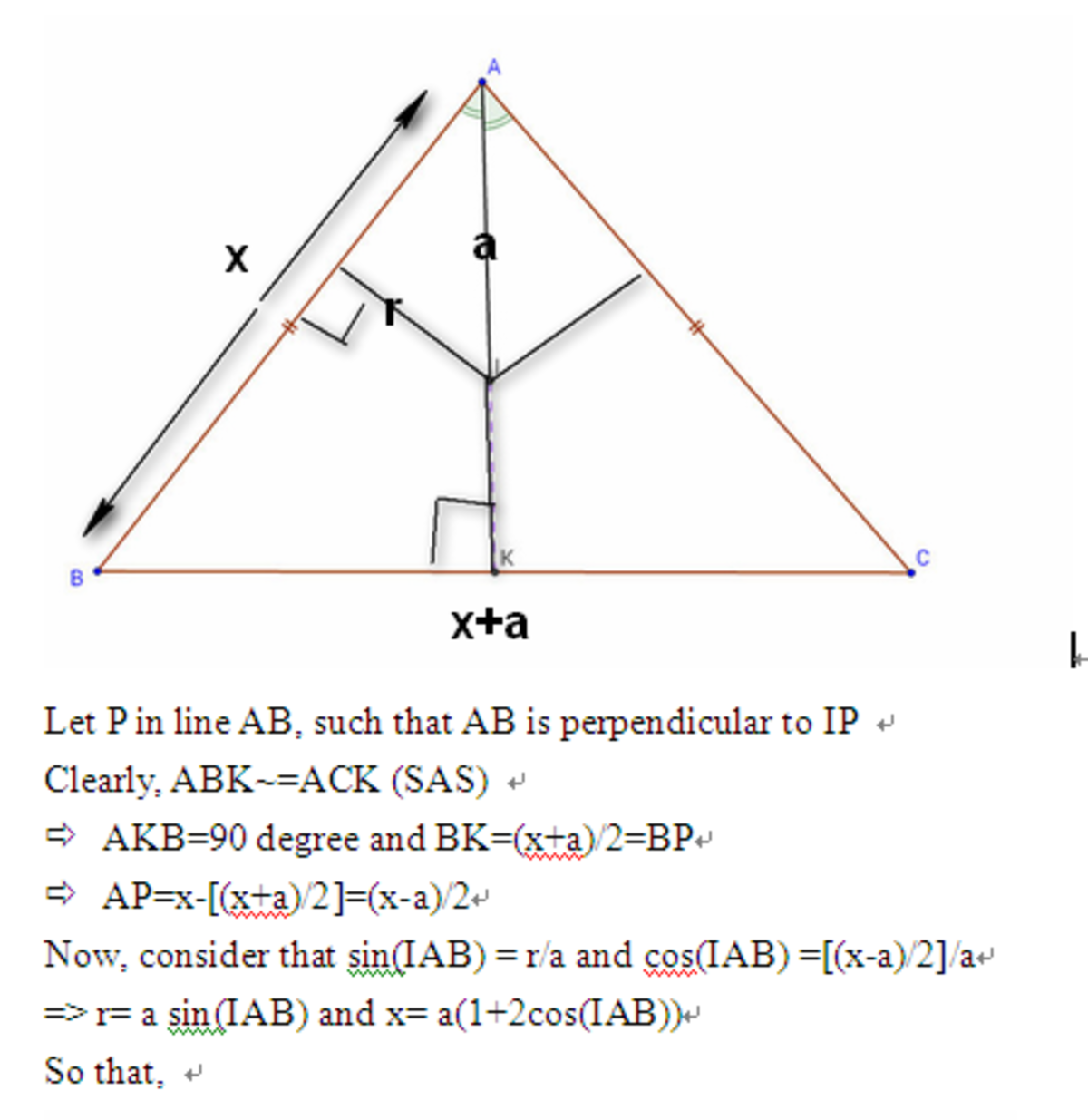
Cool geometry

Geometry Level 3

Let A B C ABC be a triangle in which A B = A C AB = AC and let I I be its incentre. Suppose B C = A B + A I BC = AB + AI . Find the value of ∠ B A C \angle BAC in degrees.


The answer is 90.

View wiki
Soumyajit Banerjee by Soumyajit Banerjee , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

汶汶 樂
Sep 19, 2015

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Ajit Athle
May 18, 2018

Refer to the given diagram. Let BK = y. Then AK = √(x²-y²) and A I I K \frac{AI}{IK} = x y \frac{x}{y} or A I A K \frac{AI}{AK} = x ( x + y ) \frac{x}{(x+y)} . In other words, AI = x √ ( x ² − y ² ) ( x + y ) \frac{x√(x²-y²)}{(x+y)} and by the given condition, x + x √ ( x ² − y ² ) ( x + y ) \frac{x√(x²-y²)}{(x+y)} =2y. We solve this to get y= x √ 2 \frac{x}{√2} . Therefore, BC=√2 x which implies AB²+AC²=BC² or that angle BAC=90°

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...