Abstract Pac Man
A quarter circle with radius 4 units has a circle inscribed in it. Find the diameter of the inscribed circle (in units). Give your answer to 3 decimal places.
The answer is 3.314.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
25 solutions
You are a genius @Pratik Soni sir upvoted
It will be best if you add graphical marked diagram
Damn silly mistake. God damned
Nice thought : )
Great solution! I used the exact same method.
how do you know that diagonal of the square and point of contact of two opposite smaller circle an d big circle are collinear . we cannot say under root 2r +2r is diagonal until we prove that the points are collinear
Nice.I almost right in this problem.
i think the question given there is wrong.... coz it has many different answers, just as ua one and one more here... draw two more small circles, join the centre of the three circle, u will get a rt trangle.. now base and the perpndicular will be equal, as they hv same length of2r = X, calculate for the hypotns,, it will be X sq + Xsq = H sq or Xsq = H,, now hyp + base =diametre of the large circle.. i, e Xsq +X = 8 or Xcube =8 or X=2, or 2r = 2 or r=1
Log in to reply
Xsq+Xsq=Hsq then sqrt2 * X = H you've written Xsq = H so sqrt2 * X + X = 8 then X= 8/(1.414+1) X=8/2.414 X=3.314
How above Xsq=H
how do you know that the triangle will pass through the centre of larger circle
Log in to reply
The triangle has to go through the center because two of its sides are the radii of the larger circle. Basic geometry.
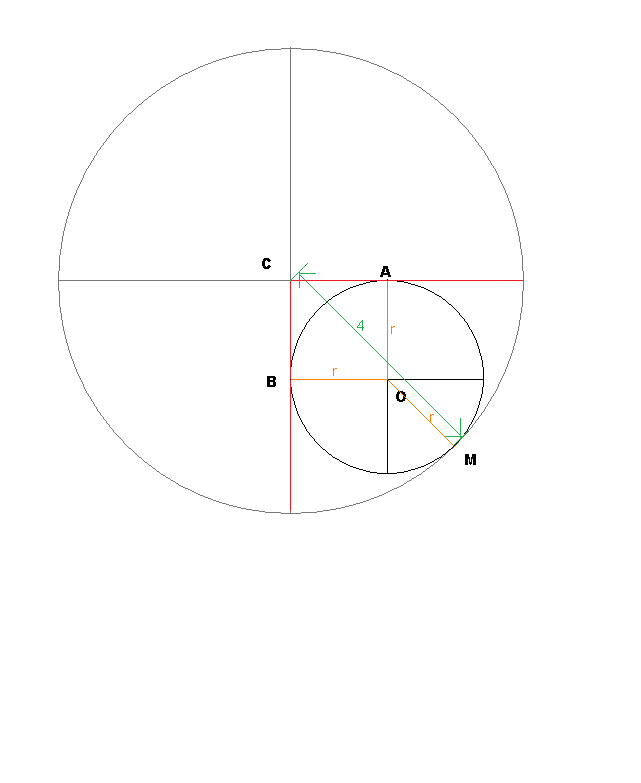
- Let the center of the small circle be O.
- Let the points where the small circle touches the red lines be A and B in any order (it's symmetrical).
- Let the point where the small circle touch the big circle be M.
- We have: O A = O B = O M = r where r is the radius of the small circle.
- Let the center of the big circle be C.
- We have C M = 4 .
- We have O C = O A 2 + O B 2 by Pythagorus' Theorem.
- We have O C = r 2 + r 2 = 2 r .
- We have O C + O M = 4 .
- Therefore we have 2 r + r = 4 .
- Therefore ( 2 + 1 ) r = 4 .
- Therefore r = 2 + 1 4 .
- Therefore the diameter is 2 + 1 8 .
I think problem is overrated
Great ....... !!!!very well explained...
Log in to reply
The solution has to be geometrically. Very well explained...it is great.......!!!.
beautifully framed answer..............
I did the same way.. just easy one.
The solution has to be geometrically. Very well explained...it is great.......!!!.
Great solution!! Upvoted ⌣ ¨
Did the same.
I did it in a similar way
How OC^2= OA^2 + OB^2
This is what exactly I did
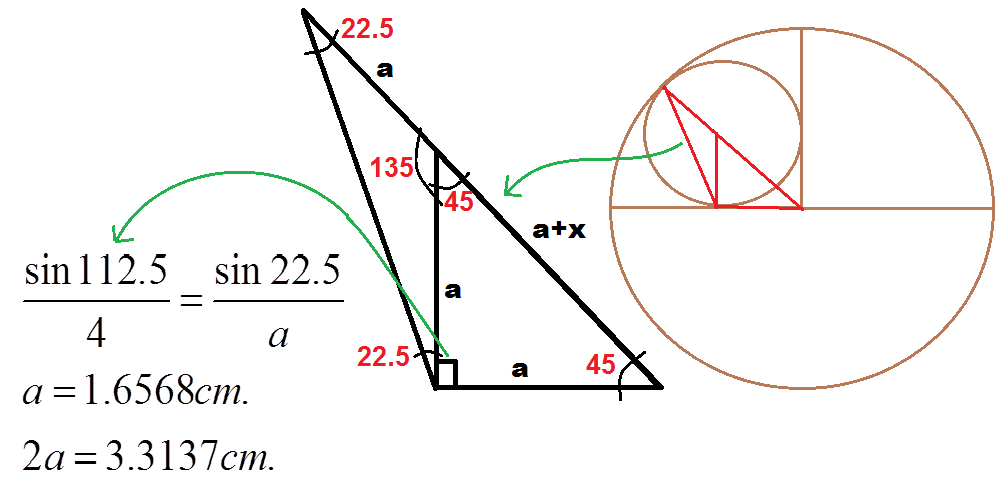
Consider right angl tri. with sides a,a,a+x. the hyp is sqrt. of a. Now dia. of larger circle=a+sqrt of a=4.solve :-).....no angles required!!!
Mine is Same method
Let the center of the bigger circle be M. Let the center of the small circle be N. Let the point of contact of the two circles be A. MN = (square root of 2) R, where R is the radius of the small circle. MA = 4 = (square root of 2) R + R Then R = 4 / [(square root of 2) + 1] = 1.656854 The diameter = 2 R = 3.3137
sir i did'nt understood why M N = 2 R ?
Log in to reply
if the two points of contact are A and B respectively then MANB will form a square because all sides will be equal and the angle between them will be 90(you can prove that by congruency of triangles) . MN will be the diagonal of the square MANB. so MN = squareroot of R.
Log in to reply
In your result but how can u decide that MA = 1/2 of R(big circle's radius) if u draw the figure it doesn't seems to be exactly half of radius it would be some less than it no doubt the MANB will be square but how can we judge or come to result that the length of sides will be 1/2 of R by drawing it in paint it seems to be answer 2.65 to 2.67
Length of the diagonal of a square= √2 times the length of the side of a square
boss...........MN=diagonal of the squir with sides equal to R
Thank you very much Mr. Gamal
I did it using a lesser known Tangent Secant Theorem
Let O be the center of the circle and A be the point when the radius of the bigger circle touches the smaller circle tangentially.
Also, let B be the point when the smaller circle touches the circumference of the bigger circle.
Join OB and let the point on which OB touches the smaller circle(circumference) only be C.
Now, by Tangent Secant Theorem,
O A 2 = ( O B ) ∗ ( O C )
Let the radius of the smaller circle be a .
a 2 = 4 ( 4 − 2 a )
a 2 + 8 a − 1 6 = 0
Now using quadratic formula,
a = 4 ( 2 − 1 )
Hence, diameter = 2 a = 8 ( 2 − 1 )
= 3 . 3 1 4
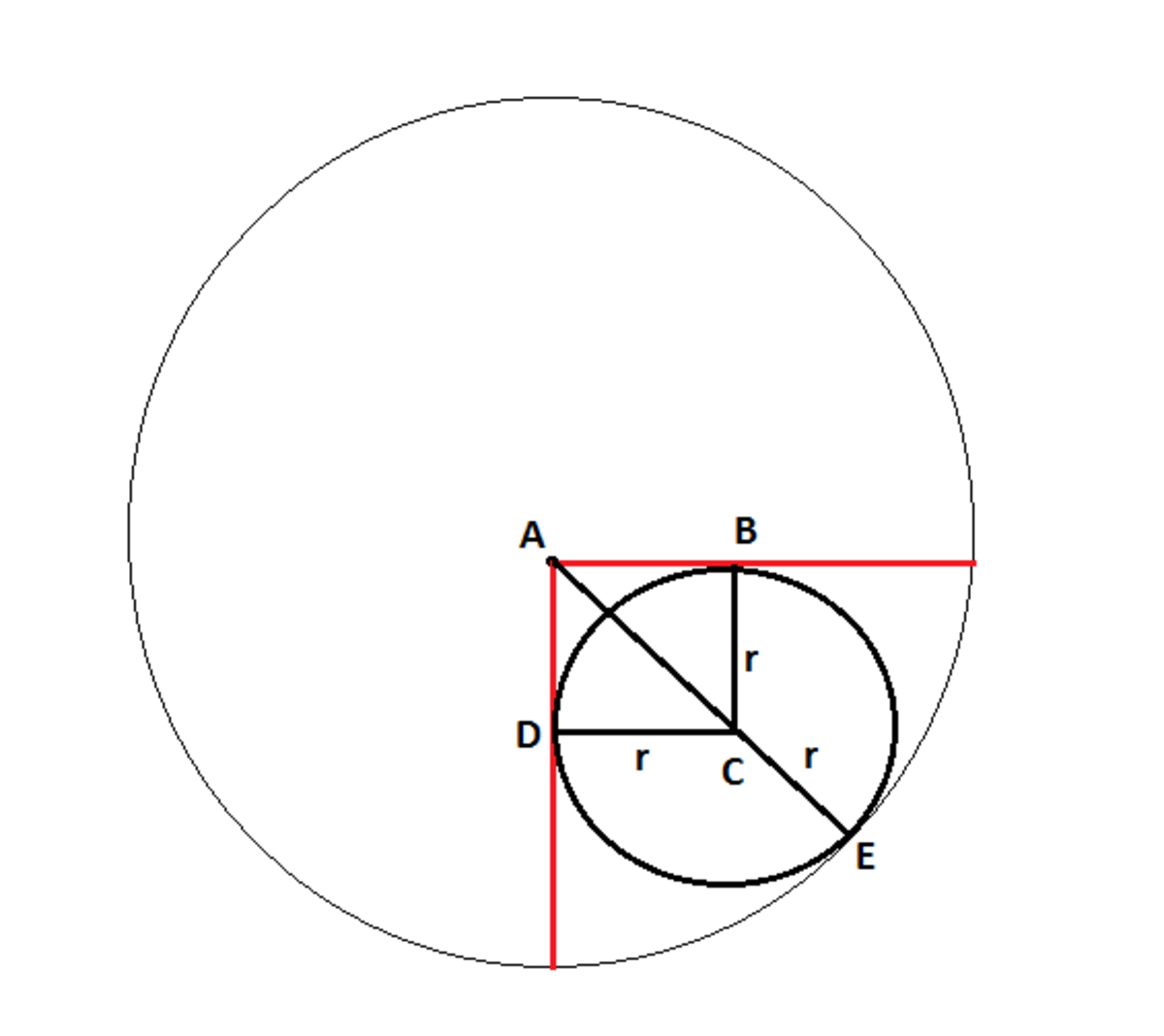
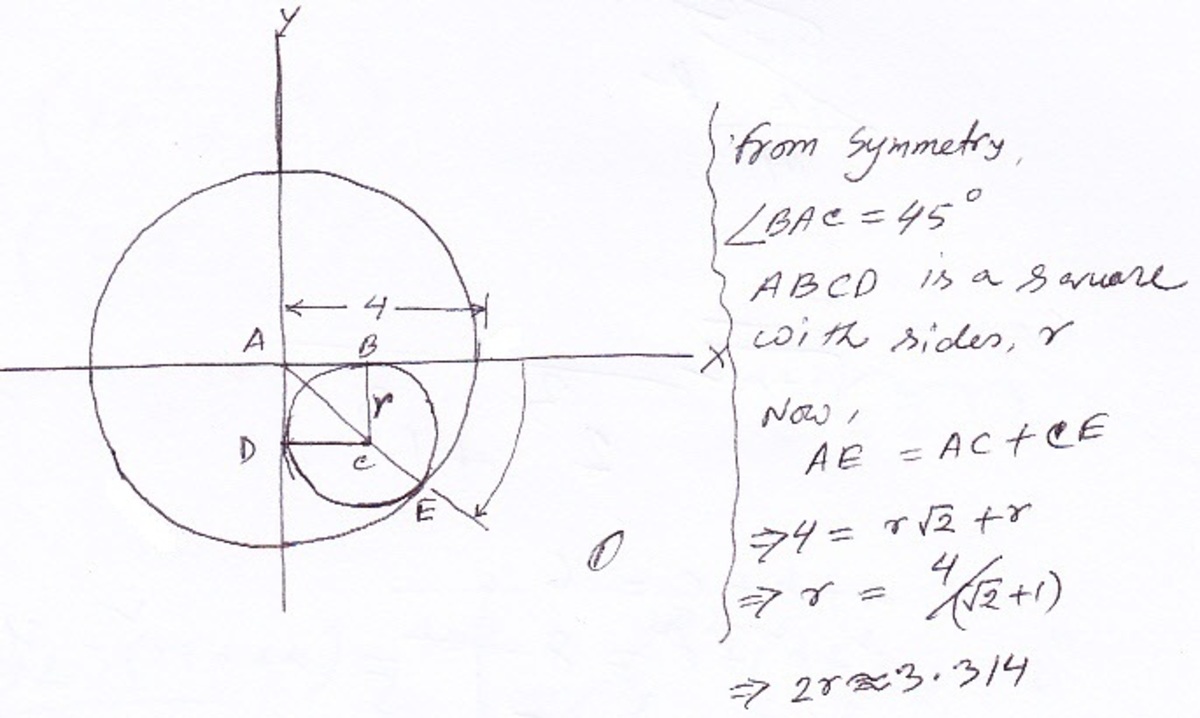
Let radius of circle be r . And ABCD is a square since all angles are right and two adjacent sides are equal.
Now, in triangle ABC, A C = 2 r . So, C E = 4 − 2 r .
But C E = r .
So, equating both and solving , we get r = 2 + 1 4 .
Diameter = 2 r = 2 + 1 8 = 3 . 3 1 4 .
Moderator note:
Simple standard approach.
Note: To type in Latex, you just need to add the brackets \ ( \ ) . I've edited your solution so you can see how it's done. You got all of the Latex phrasing correct!
Same method. High five!
Lets put the circles in a cartesian space, with the centre of the larger circle at (0,0). The two radii in red are (4,0) and (0,-4) of course. Since the smaller circle is in the 4th quadrant, the centre will be at (r,-r) and the tangents touching the radii are at (r,0) and (0,-r) resp. This implies that 0 < r < 4.
Now. Lets form equations of the two circles:
x² + y² = 16 --> 1
(x - r)² + (y + r)² = r² --> 2
We will use these later.
Note that the line joining the centre of two circles and the meeting point of two circles fall on the same line. And the angle is -45˚. Therefore the equation of this line is
y = -x --> 3
and this satisfies equations 1 and 2.
Solving with equation 1, we get the tangent point to be (2√2 , -2√2)
Using these values in Equation 2, we get
r = 4(√2 - 1)
Therefore diameter = 8(√2 - 1) = 3.3137
you are great !
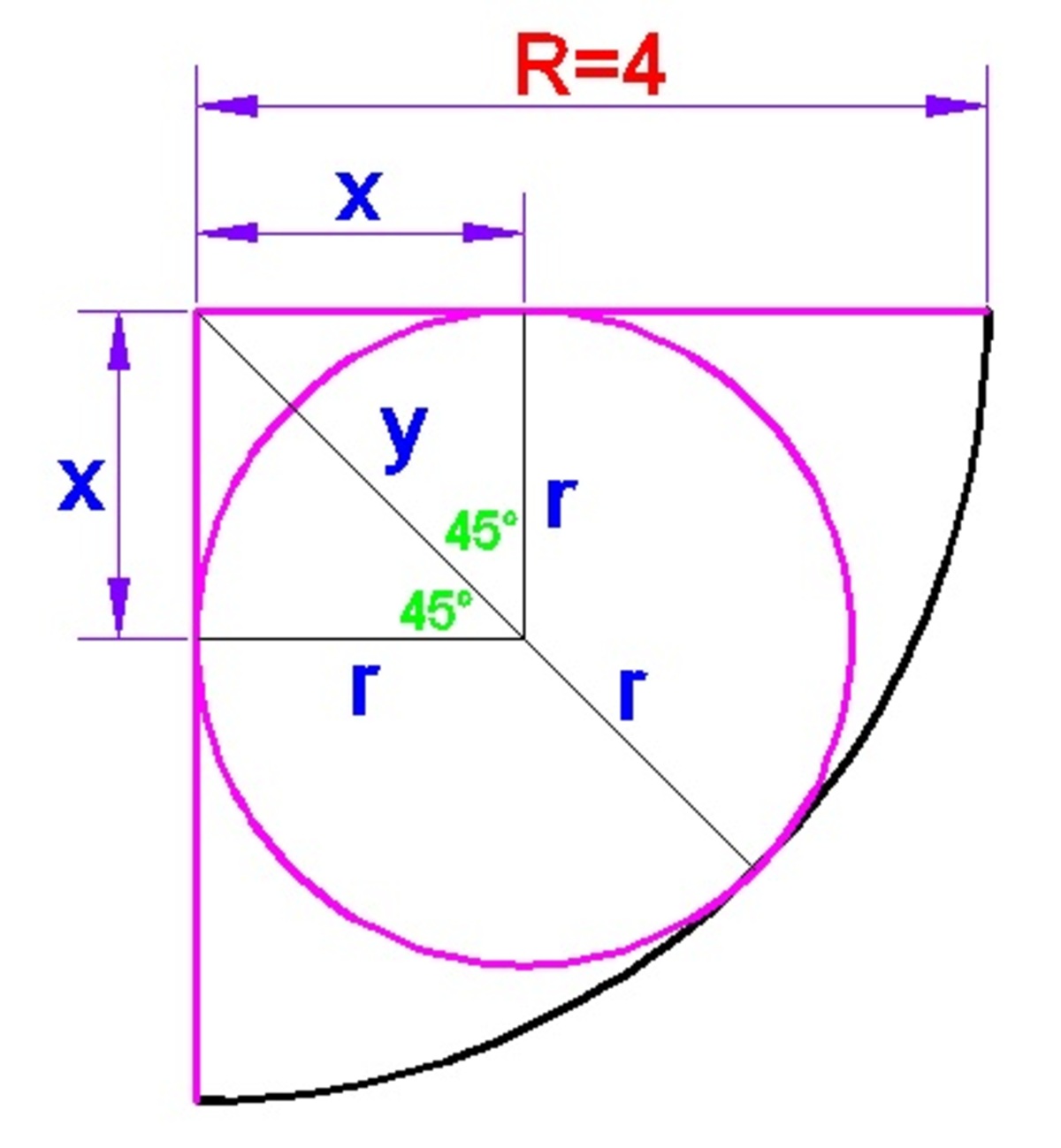 t
a
n
4
5
=
r
x
=
1
t
a
n
4
5
=
r
x
=
1
x = r
y = 4 − r
By Pythagorean Theorem, we have
y 2 = x 2 + r 2
But we know that x = r and y = 4 − r , so we substitute
( 4 − r ) 2 = r 2 + r 2
1 6 − 8 r + r 2 = 2 r 2
1 6 − 8 r = r 2
r 2 + 8 r − 1 6 = 0
By using the quadratic formula, we have
r = 4 ( 2 − 1 ) = 1 . 6 5 7 u n i t s
d = 2 r = 2 ( 1 . 6 5 7 ) = 3 . 3 1 4 u n i t s
The best solution so far.
Draw radius from Center of Bigger circle through center of smaller circle. This will bisect the quadrant, let us call it 'L'
Draw a perpendicular from one of the tangent of smaller circle to center of smaller circle.
Let us say radius of smaller circle is r
L = r + x
and we have x r = cos 4 5 = 2 1
By Substitution you get
r = ( 1 + 2 ) 4
So diameter d = 2 r = 3 . 3 1
Treat it as an optimisation problem. Think of a family of circles starting as a point at the origin growing to fill the quadrant. If the radius of one of these circles is r then the formula for the distance from the origin to the outer edge of the circle is straightforward and can be compared with the radius of the larger circle. Then minimise the difference between these two values.
Use cartesion method assume centre of big circleA(0,0)and centre of smaller circleB(r,-r) ,where 'r' is the radius of smaller circle. And distance between both centres is(4-r)=d. Now apply AB=d. By this u can get value of r and now find the diametre 2r.
- R = 4
- r = radius of small circle
- d = 2 r = diameter of small circle R r d = 2 r r = r + r 2 + r 2 = r + r 2 = r ( 1 + 2 ) = 1 + 2 R = 1 + 2 2 R = 1 + 2 2 ( 4 ) ≈ 3 . 3 1 3 7 0 8 4 9 9 5 ≈ 3 . 3 1 4
A typo, it's d ≈ 3 . 3 1 4
Let A be the center of the big circle, B the point of contact between the small circle and a radius of the big circle, D the contact point between the two circles, and C the intersection of AD with the small circle.
AB×AB=AC×AD r^2=4 (4-2r) So r=4 (sqrt (2)-1) Diameter=2r~3.3137
let the distance from the circle center to the point such that the inside circle touch the radius be x so the distance between the circle center and its circumference is R = 4 units thus x 2 + x 2 + x = R = 4
( 2 + 1 ) x = 4
diameter is twice the radius so
d = 2 x = 2 + 1 8 = 3 . 3 1 3 7
Over Rated problem. Does not deserve level 5
4 = r + 2 r
2 r = 1 + 2 8
d = 8 ( 2 -1) = 3.3137084989847603904135097936776+
Answer: 3 . 3 1 4
As far as the figure given is concerned, I assume that the center of the inscribed circle can be approximately by getting its centroid, though this is not a good solution.
Formula for centroid of quarter circle 3 π 4 r = 3 π 4 ( 4 ) ≈ 1 . 6 9 the value of radius and 3 . 3 8 will be its diameter, almost an approximate value to the real diameter which is 2 + 1 8 ≈ 3 . 3 1
This problem is extremely overrated!
8 = r + r 2sq.root of 2r + r r = 1.657
It's a damn shame that this is a level 5 prob.
I used Co-ordinate Geometry (Long but different method), as it seemed to me. Let center of large circle be (0,0). Let radius of small circle be 'r' which implies (r,-r) will be centre of small circle. So, equation of line passing through (r,-r) and (0,0) becomes X+Y=0. Equation of bigger circle is X 2 + Y 2 = 1 6 . Intersection point of the both these equations will be ( 8 , − 8 ). As radius of small circle is same all the ways, drop a perpendicular from centre of smaller circle to the radius of larger cicle, in which it is inscribed. That point will be (r,0).Calculate distance between (r,-r) and (r,0).Calculate distance between (r,-r) and ( 8 , − 8 ). We will now equate these two distances, we get a quadratic equation in 'r' as r 2 − 4 8 r + 1 6 = 0 . Solving it, we get r= 4( 2 − 1 ) . So, 2r= diameter of smaller circle = 8( 2 − 1 ) which equals 3.313 .. (approx).
Not a level 5 problem. It should have been a level 3 problem. Just following basic geometry concepts.
If we join the point of tangecy with the diametral opposite point of extrem of one radius, this line touch the other radius un the other ponit of tangecy, form homothety. Just use basic trigonometry and its done.
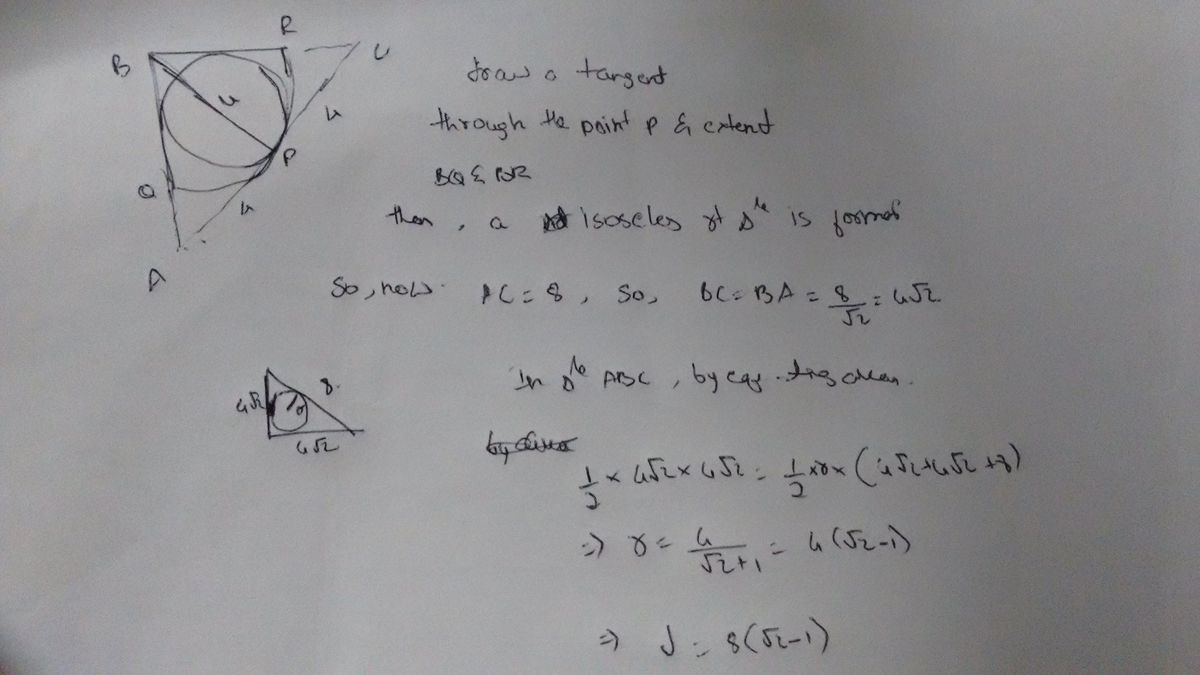
draw the remaining 3 circles inside the circle(so each quarter has a small circle).
So you have 4 touching circles.
the centers of these 4 small circles form a square.
the side of the square would be 2r (r is the radius of the smaller circle)
the diagonal of the square + 2r = diameter of the larger circle
2r sqrt{2} + 2r = 8
Solving for 2r,
2r = 8/(sqrt{2} + 1) approx 3.3137