Googly Eyes
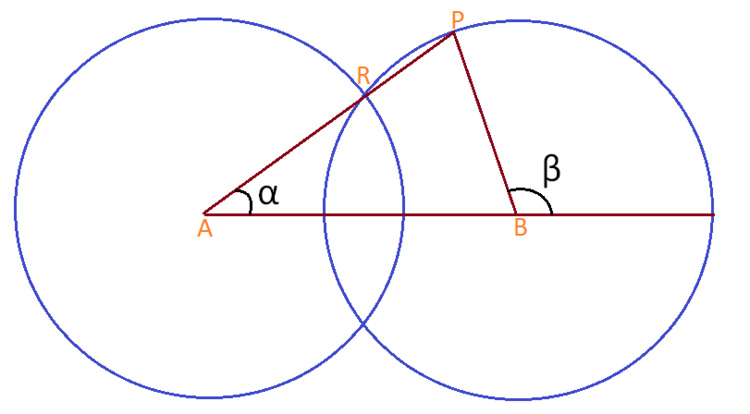 In the above diagram, two circles of radius
intersect, and the distance between their centers is greater than
. Angles
and
are defined as above.
In the above diagram, two circles of radius
intersect, and the distance between their centers is greater than
. Angles
and
are defined as above.
Which of the following is true?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Letting R be the (upper) point of intersection of the two circles as shown in the diagram, we see that, by symmetry, ∠ A B R = ∠ B A R = α , (since the two circles have the same radius). Thus ∠ A R B = π − 2 α , and so ∠ B R P = 2 α .
Since Δ B R P is isosceles with B R = B P we have that ∠ B P R = ∠ B R P = 2 α , and so ∠ P B R = π − 4 α .
Finally, β = π − ∠ P B R − ∠ A B R = π − ( π − 4 α ) − α = 3 α .
Thus β = 3 α is the correct option.