Use only Holder's

For those who dont know Holder's inequality, just use power mean inequality...

$(\frac{a^{2015}+b^{2015}}{2})^{\frac{1}{2015}}\geq \frac{a+b}{2}$

And the rest follows naturally.

Use the Holder's inequality:

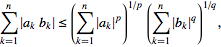
suppose a and b be the terms of sequence $a_{k}$ as per the above inequality. consider a as the first term and b as the second term of this sequence. Let's assume that: sequence $b_{k}$ = {1,1,1,1....} i.e. every term is 1. Now, for n=2, p=2015 and q=1, we can write:

$\sum_{i=1}^2 |a_{k}|<=(\sum_{i=1}^2 (a_{k})^{2015})^{1/2015}.(\sum_{i=1}^2 1)$
$a+b<=2(a^{2015}+b^{2015})^{1/2015}$
$a+b<=2.(2015)^{1/2015}$
hence $a+b <= 2.007566012$

Thus the maximum value of a + b is 2.007566012

Using Holder's Inequality we have

$\large{\left( { a }^{ 2015 }+{ b }^{ 2015 } \right) \left( 1+1 \right) \left( 1+1 \right) \cdots \cdots \cdots \left( 1+1 \right) \ge { \left( a+b \right) }^{ 2015 }}$ .

It is similar as Cauchy Schwarz Inequality but here I increased the power from $2$ to $2015$ and same with the terms.

$\large{\sqrt [ 2015 ]{ 2015\times { 2 }^{ 2014 } } \ge \left( a+b \right) =2.006}$

I will use generalised form of Titu's Lemma.

Given condition is :

$\dfrac{{a}^{2015}}{1^{2014}} + \dfrac{b^{2015}}{1^{2014}} = 2015$

Using generalised form of Titu's Lemma , we get :

$2015 \ge \dfrac{[a+b]^{2015}}{[1+1]^{2014}}$

So,

$(2)^{\frac{2014}{2015}}(2015)^{\frac{1}{2015}} \ge a+b$

Hence ,

$a+b \le 2.006$

((1+1)^(2014/2015))×(given expression) >= a+b. Tis is by Holder's inequality.

Here is a solution by calculus.

WLG, Let's assume $a \geq b$ , so - $2015^{\frac{1}{2015}} \geq a \geq b \geq 0$ $b = \left(2015 - a ^ {2015}\right)^{\frac{1}{2015}}$ $S = a + b = a + \left(2015 - a ^ {2015}\right)^{\frac{1}{2015}}$ $\frac{dS}{da} = 0 \Rightarrow \boxed{a = \left(\frac{2015}{2}\right)^{\frac{1}{2015}}}$ $\Rightarrow \boxed{b = \left(\frac{2015}{2}\right)^{\frac{1}{2015}}}$ This pair of $(a, b)$ may be just a local extremum, so we check with boundary case. Which is $a = 2015^{\frac{1}{2015}}$

Among boundary case and local extremum values, $\boxed{2\times \left(\frac{2015}{2}\right)^{\frac{1}{2015}} = 2.00687554}$ is optimal solution for $a = b = \left(\frac{2015}{2}\right)^{\frac{1}{2015}}$