A geometry problem by Ahmed Moh AbuBakr

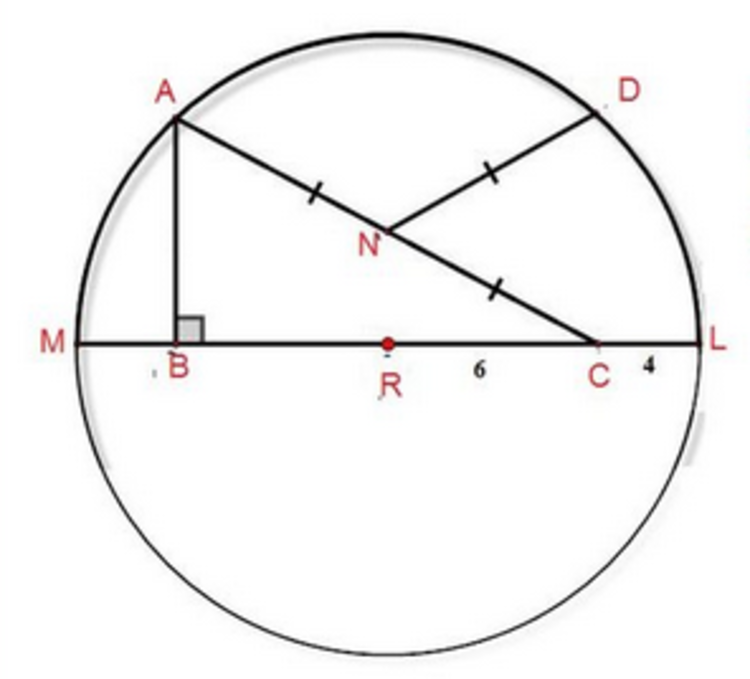Simply you have x=rcos(angle) so the cosine of the angle is equal to 3/5( because the radius is 10 and x=6). With the same logic y=rsin(angle) then y=10(4/5)=8. Obviuosly i can do that because ADBC is a rectangle( by the property of the median of a right angled triangle)

It is assumed that $R$ is the center of the circle and that $ML$ is a diameter.

Since $\Delta ABC$ is a right triangle and $N$ is the midpoint of $AC,$ we know that $|BN| = |AN|.$ Also, since $|DN| = |AN| = |NC|$ and $D$ lies on the circle, we know that, by symmetry, $BN$ and $ND$ joined together form a straight line. Thus the quadrilateral $ABCD$ is a rectangle inscribed in a semicircle, and so $R,$ as the center of the circle, must also be the midpoint of $BC.$

Now place $R$ at the origin of an $xy$ -grid and orient the circle so that $BC$ lies along the $x-$ axis. Then since the radius $|RL|$ of the circle is $6 + 4 = 10,$ the equation of the circle is $x^{2} + y^{2} = 100.$

Finally, as $|BR| = |RC| = 6,$ the coordinates of $A$ will be $(-6,A_{y}),$ and since $A$ lies on the circle we know that $(-6)^{2} + A_{y}^{2} = 100 \Longrightarrow A_{y} = 8,$ and so $|AB| = \boxed{8}.$

Draw a right triangle $MAL$ with $\angle{MAL}=90$

Then by right triangle altitude theorem: $\frac{4}{x}=\frac{x}{16}$ where $x=AB$

Solving this gives $x=\boxed{8}$