cool wedge
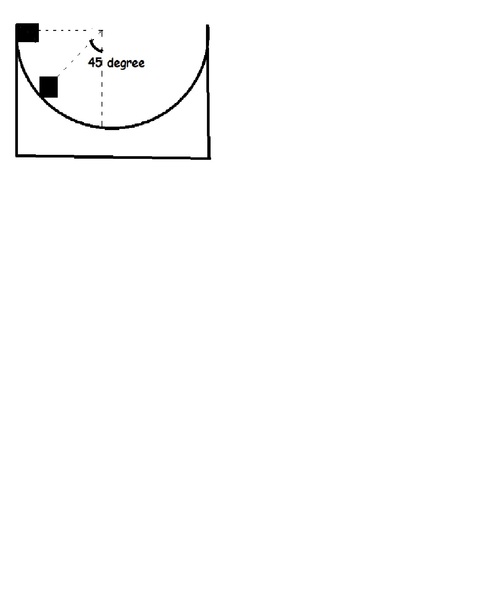A semicircular wedge of radius 'R' and mass 'M' is kept on a smooth floor free to slide.
A block of mass 'M' is kept at the top of the wedge. The system is released from rest.
Find the velocity of the wedge when line joining the center of the semicircle and the block makes 45 degree with the vertical as shown in the figure.
Details and assumptions: -
M=1Kg ,
R=1metre ,
acceleration due to gravity=10m/s*s
Give your answer correct to one decimal place.
The answer is 1.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Let the velocity of wedge be V with respect to ground. By conservation of momentum in the horizontal direction , the velocity of block in vertical direction will also be v with respect to the ground. With respect to the wedge the block is moving in the tangential direction to the circle at any instant. Therefore at the instant when the block is at 45 degree it can be assumed that it is moving down an inclined plane of inclination 45 degree. Therefore the vertical and horizontal component of velocity of the block(with respect to the wedge) should be equal. By using the concept of relative motion we can easily see that the horizontal component of velocity of the block (with respect to the wedge) is equal to 2v. Therefore the vertical component should also be equal to 2v. Now as we know the velocity of the block with respect to the wedge, we can easily find velocity of the block with respect to the ground. Now we can use the work energy theorem on the block and the wedge to get the value of v.